题目内容
如图是多面体 和它的三视图.
和它的三视图.
(1)若点 是线段
是线段 上的一点,且
上的一点,且 ,求证:
,求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)证明见解析;
(2)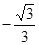
解析试题分析:(1)利用已知的线面垂直关系建立空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明线面垂直,需证线线垂直,只需要证明直线的方向向量垂直;(3)把向量夹角的余弦值转化为两平面法向量夹角的余弦值;(4)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:解:(1)由题意知AA1,AB,AC两两垂直,建立如图所示的空间直角坐标系,则A(0,0,0),A1(0,0,2),B(-2,0,0),C(0,-2,0),C1(-1,-1,2),则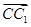 =(-1,1,2),
=(-1,1,2),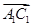 =(-1,-1,0),
=(-1,-1,0),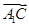 =(0,-2,-2).(1分)
=(0,-2,-2).(1分)
设E(x,y,z),则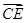 =(x,y+2,z),
=(x,y+2,z), =(-1-x,-1-y,2-z).(3分)
=(-1-x,-1-y,2-z).(3分)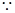
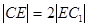

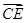 =2
=2 ,得E(
,得E(

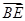 =
=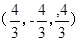
设平面C1A1C的法向量为m=(x,y,z),则由 ,
,
得 ,取x=1,则y=-1,z=1.故m=(1,-1,1),
,取x=1,则y=-1,z=1.故m=(1,-1,1),
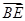 =
=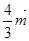 ,
, BE⊥平面A1CC1.(6分)
BE⊥平面A1CC1.(6分)
(2)由(1)知,平面C1A1C的法向量为m=(1,-1,1)
而平面A1CA的一个法向量为n=(1,0,0),则cos〈m,n〉=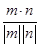 =
= =
= ,故二面角
,故二面角 的余弦值
的余弦值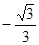 .(12分)
.(12分)
考点:利用空间向量证明垂直和夹角问题.

练习册系列答案
相关题目
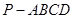 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中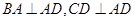 ,
, ,平面
,平面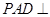 底面
底面 是
是 的中点.
的中点.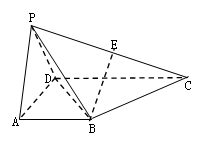
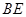 //平面
//平面 ;
;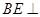
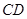 ;
;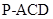 的体积
的体积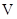 .
. 平面PCD;
平面PCD;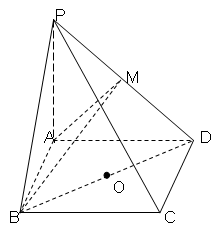
 的直观图及三视图如图所示,
的直观图及三视图如图所示,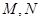 分别为
分别为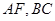 的中点.
的中点.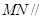 平面
平面 ;
;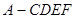 的体积.
的体积.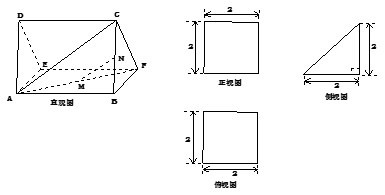
 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ .
.
 中,
中, ,
, ,
, °,平面
°,平面 平面
平面 ,
, ,
, 分别为
分别为 ,
, 中点.
中点. ∥平面
∥平面 ;
; ;
; 的体积.
的体积.
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
,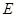 为棱
为棱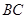 的中点,求
的中点,求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
 的度数为 .
的度数为 .