题目内容
(本题满分16分)函数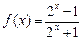 (
(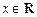 ).
).
(1)求函数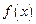 的值域;
的值域;
(2)判断并证明函数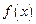 的单调性;
的单调性;
(3)判断并证明函数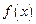 的奇偶性;
的奇偶性;
(4)解不等式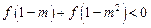 .
.
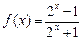 (
(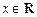 ).
).(1)求函数
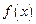 的值域;
的值域;(2)判断并证明函数
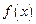 的单调性;
的单调性;(3)判断并证明函数
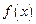 的奇偶性;
的奇偶性;(4)解不等式
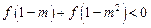 .
.(1)单调增函数
(2)奇函数
(3)
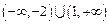
.(1)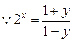 , 又
, 又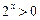 ,
,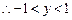 .∴函数
.∴函数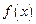 的值域为
的值域为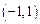 .……5分
.……5分
(2)函数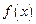 在
在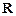 上为单调增函数.
上为单调增函数.
证明: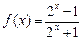 =
=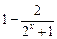
在定义 域中任取两个实数
域中任取两个实数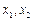 ,且
,且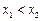 ,则
,则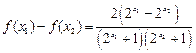 .
.
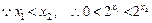 ,从而
,从而
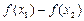
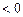 .∴函数
.∴函数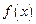 在
在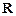 上为单调增函数.……10分
上为单调增函数.……10分
(3)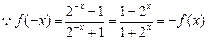 , ∴函数
, ∴函数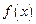 为奇函数.……13分
为奇函数.……13分
∴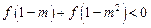 即
即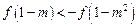 ,
,
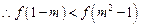
 ,
,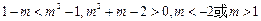 .
.
∴原不等式的解集为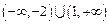 .……16分
.……16分
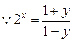 , 又
, 又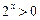 ,
,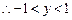 .∴函数
.∴函数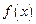 的值域为
的值域为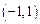 .……5分
.……5分(2)函数
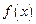 在
在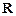 上为单调增函数.
上为单调增函数.证明:
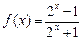 =
=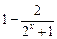
在定义
 域中任取两个实数
域中任取两个实数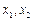 ,且
,且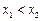 ,则
,则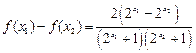 .
.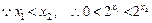 ,从而
,从而
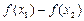
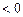 .∴函数
.∴函数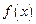 在
在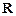 上为单调增函数.……10分
上为单调增函数.……10分(3)
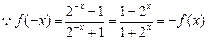 , ∴函数
, ∴函数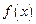 为奇函数.……13分
为奇函数.……13分∴
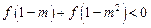 即
即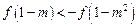 ,
,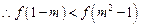
 ,
,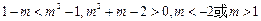 .
.∴原不等式的解集为
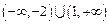 .……16分
.……16分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
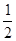 )
)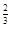 <(
<(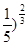 <(
<(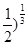 B (
B (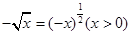
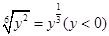
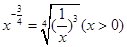
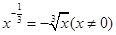
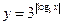 的图象大致是 ( )
的图象大致是 ( )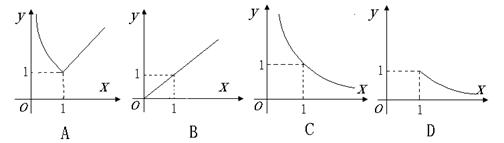
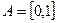 ,设函数
,设函数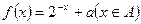 的值域为
的值域为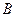 ,若
,若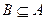 ,则实数
,则实数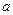 的取值范围是___________.
的取值范围是___________. ,下列等式一定成立的是( )
,下列等式一定成立的是( ) (
( (
( (
(
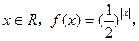 若不等式
若不等式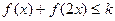 对于任意的
对于任意的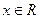 恒成立,则实数
恒成立,则实数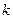 的取值范围是 .
的取值范围是 . 的图象
的图象 的大致形状是 ( )
的大致形状是 ( )
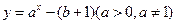 的图象不经过第一象限,则
的图象不经过第一象限,则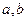 满足条件为_______
满足条件为_______