题目内容
对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:①f(x1+x2)=f(x1)•f(x2);
②f=f(x1)+f(x2);
③
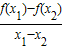 >0;
>0;④
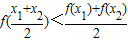 .
.当f(x)=lgx时,上述结论中正确结论的序号是 .
【答案】分析:利用对数的基本运算性质进行检验:①f(x1+x2)=lg(x1+x2)≠f(x1)f(x2)=lgx1•lgx2,②f(x1•x2)=lgx1x2=lgx1+lgx2=f(x1)+f(x2)③f(x)=lgx在(0,+∞)单调递增,可得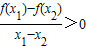
④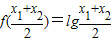 ,
,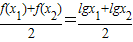 =
=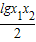 ,由基本不等式可得
,由基本不等式可得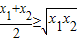 从而可得
从而可得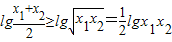
解答:解:①f(x1+x2)=lg(x1+x2)≠f(x1)f(x2)=lgx1•lgx2
②f(x1•x2)=lgx1x2=lgx1+lgx2=f(x1)+f(x2)
③f(x)=lgx在(0,+∞)单调递增,则对任意的0<x1<x2,d都有f(x1)<f(x2)
即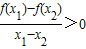
④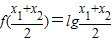 ,
,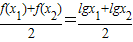 =
=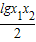
∵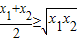 ∴
∴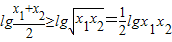
故答案为:②③
点评:本题主要考查了对数的基本运算性质,对数函数单调 性的应用,基本不等式的应用,属于知识的简单综合应用.
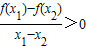
④
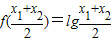 ,
,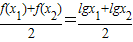 =
=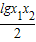 ,由基本不等式可得
,由基本不等式可得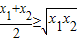 从而可得
从而可得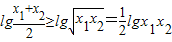
解答:解:①f(x1+x2)=lg(x1+x2)≠f(x1)f(x2)=lgx1•lgx2
②f(x1•x2)=lgx1x2=lgx1+lgx2=f(x1)+f(x2)
③f(x)=lgx在(0,+∞)单调递增,则对任意的0<x1<x2,d都有f(x1)<f(x2)
即
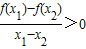
④
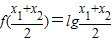 ,
,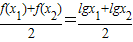 =
=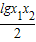
∵
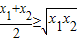 ∴
∴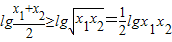
故答案为:②③
点评:本题主要考查了对数的基本运算性质,对数函数单调 性的应用,基本不等式的应用,属于知识的简单综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目