题目内容
设x1、x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a＞0)的两个极值点.(1)若x1=-1,x2=2,求函数f(x)的解析式;
(2)若|x1|+|x2|=22,求b的最大值;
(3)设函数g(x)=f′(x)-a(x-x1),x∈(x1,x2),当x2=a时,求证:|g(x)|≤
a(3a+2)2.
(1)解:∵f(x)=ax3+bx2-a2x(a＞0),
∴f′(x)=3ax2+2bx-a2(a＞0).
依题意有
∴
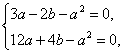a＞0.
解得
∴f(x)=6x3-9x2-36x.
(2)解:∵f′(x)=3ax2+2bx-a2(a＞0),
依题意,x1,x2为方程f′(x)=0的两个根,且|x1|+|x2|=2
,
∴(x1+x2)2-2x1x2+2|x1x2|=8.
∴(
)2-2(
)+2|
|=8.
∴b2=3a2(6-a).
∵b2≥0,∴0＜a≤6.
设p(a)=3a2(6-a),则p′(a)=-9a2+36a.
由p′(a)＞0得0＜a＜4,由p′(a)＜0得a＞4,
即函数p(a)在区间(0,4］上是增函数,在区间［4,6］上是减函数.
∴当a=4时,p(a)有极大值为96.
∴p(a)在(0,6］上的最大值是96.
∴b的最大值为4
.
(3)证明:∵x1,x2是方程f′(x)=0的两根,
∴f′(x)=3a(x-x1)(x-x2).
∵x1·x2=
,x2=a,
∴x1=
.
∴|g(x)|=|3a(x+
)(x-a)-a(x+
)|
=|a(x+
)［3(x-a)-1］|.
∵x1＜x＜x2,即
＜x＜a,
∴|g(x)|=a(x+
)(-3x+3a+1).
∴|g(x)|=-3a(x+
)(x
)
=-3a(x
)2+
+a2+
a
≤
+a2+
a=
.
∴|g(x)|≤
(3a+2)2成立.
练习册系列答案
相关题目
，求实数b的最大值；