题目内容
已知直线L:y=
x+m与曲线C:y=
仅有三个交点,则实数m的取值范围是( )
| 1 |
| 2 |
| 1 |
| 2 |
| |4-x2| |
A、(-2,
| ||||
B、(-
| ||||
C、(1,
| ||||
D、(1,
|
分析:分析曲线C的方程y=
可得是椭圆的上半部分与双曲线的上半部分,由图形可得找出两个临界值即直线平移到(0,1)与直线和椭圆相切(△=16m2-8(4m2-4)=0)的时候,得到答案.
| 1 |
| 2 |
| |4-x2| |
解答:解:由题意得曲线C:y=
∴2y=
即4y2=|4-x2|(y≥0)
当4-x2≥0时得到4y2=4-x2即
+y2=1(y≥0)
当4-x2<0时得到
-y2=1(y≥0)
由以上可得曲线C的图形为
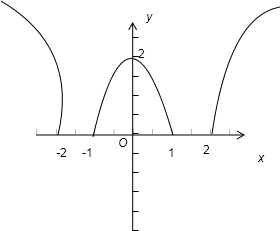
∵直线L:y=
x+m与双曲线
-y2=1的渐近线平行
∴把直线y=
x向上平移平移到(0,1)点时有两个交点,此时m=1.继续向上平移则有3个交点.
当直线与椭圆的上半部分相切时此时有两个交点.
联立直线与椭圆的方程
代入整理得2x2+4mx+4m2-4=0
△=16m2-8(4m2-4)=0即m=
或-
(舍去)
由图示可得m=
由以上可得1<m<
故答案为C.
| 1 |
| 2 |
| |4-x2| |
∴2y=
| |4-x2| |
即4y2=|4-x2|(y≥0)
当4-x2≥0时得到4y2=4-x2即
| x2 |
| 4 |
当4-x2<0时得到
| x2 |
| 4 |
由以上可得曲线C的图形为

∵直线L:y=
| 1 |
| 2 |
| x2 |
| 4 |
∴把直线y=
| 1 |
| 2 |
当直线与椭圆的上半部分相切时此时有两个交点.
联立直线与椭圆的方程
|
△=16m2-8(4m2-4)=0即m=
| 2 |
| 2 |
由图示可得m=
| 2 |
由以上可得1<m<
| 2 |
故答案为C.
点评:解决此类问题的根据是灵活运用平面几何的相关知识与结论,结合图形解决问题,即数形结合的是想是高中数学的一个重点也是高考必考的知识点.

练习册系列答案
相关题目
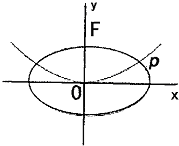 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: