题目内容
(第一、二层次学校的学生做)
对于函数f(x)=ax2+bx+1(a>0),如果方程f(x)=x有相异两根x1,x2.
(1)若x1<1<x2,且f(x)的图象关于直线x=m对称.求证:m>
;
(2)若0<x1<2且|x1-x2|=2,求证:4a+2b<1;
(3)α、β为区间[x1,x2]上的两个不同的点,求证:2aαβ-(1-b)(a+β)+2<0.
对于函数f(x)=ax2+bx+1(a>0),如果方程f(x)=x有相异两根x1,x2.
(1)若x1<1<x2,且f(x)的图象关于直线x=m对称.求证:m>
| 1 |
| 2 |
(2)若0<x1<2且|x1-x2|=2,求证:4a+2b<1;
(3)α、β为区间[x1,x2]上的两个不同的点,求证:2aαβ-(1-b)(a+β)+2<0.
(1)设g(x)=ax2+(b-1)x+1,且a>0
∵x1<1<x2,∴(x1-1)(x2-1)<0,即x1x2<x1+x2-1,
于是x=m即x=-
,也就是x=
(-
-
)
∴m=
(-
-
)=
(x1+x2)-
x1x2>
(x1+x2)-
[(x1+x2)-1]=
即不等式m>
成立;
(2)由方程g(x)=ax2+(b-1)x+1=0,可得x1x2=-
>0,故x1、x2同号
由0<x1<2且|x1-x2|=2,得x2-x1=2
∴x2=x1+2>2,
由此可得2∈(x1,x2),得g(2)<0,
所以4a+2b-1<0,可得4a+2b<1;
(3)由前面的结论,得x1+x2=
,x1x2=
α、β为区间[x1,x2]上的两个不同的点,不妨设α<β
0>2(α-x1)(β-x2)
∵2(α-x1)(β-x2)=2αβ-2(βx1+αx2)+2x1x2
=2αβ-(x1+x2)(α+β)+2x1x2+(x1-x2)(α-β)>2αβ-(x1+x2)(α+β)+2x1x2
且2αβ-(x1+x2)(α+β)+2x1x2=
∴0>
,
结合a>0,可得2aαβ-(1-b)(a+β)+2<0.
∵x1<1<x2,∴(x1-1)(x2-1)<0,即x1x2<x1+x2-1,
于是x=m即x=-
| b |
| 2a |
| 1 |
| 2 |
| b-1 |
| a |
| 1 |
| a |
∴m=
| 1 |
| 2 |
| b-1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即不等式m>
| 1 |
| 2 |
(2)由方程g(x)=ax2+(b-1)x+1=0,可得x1x2=-
| 1 |
| a |
由0<x1<2且|x1-x2|=2,得x2-x1=2
∴x2=x1+2>2,
由此可得2∈(x1,x2),得g(2)<0,
所以4a+2b-1<0,可得4a+2b<1;
(3)由前面的结论,得x1+x2=
| -b+1 |
| a |
| 1 |
| a |
α、β为区间[x1,x2]上的两个不同的点,不妨设α<β
0>2(α-x1)(β-x2)
∵2(α-x1)(β-x2)=2αβ-2(βx1+αx2)+2x1x2
=2αβ-(x1+x2)(α+β)+2x1x2+(x1-x2)(α-β)>2αβ-(x1+x2)(α+β)+2x1x2
且2αβ-(x1+x2)(α+β)+2x1x2=
| 2aαβ-(1-b)(α-β)+2 |
| a |
∴0>
| 2aαβ-(1-b)(α-β)+2 |
| a |
结合a>0,可得2aαβ-(1-b)(a+β)+2<0.

练习册系列答案
相关题目
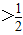 ;
;