题目内容
已知数列{an}满足:a1=1,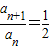 ,则数列{an}是( )
,则数列{an}是( )A.递增数列
B.递减数列
C.摆动数列
D.常数列
【答案】分析:由题意知,得到连续两项的比值等于大于0且小于1常数,得到数列是一个递减的等比数列.
解答:解:由于数列{an}满足:a1=1,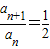 ,
,
则数列的后一项为前一项的 ,且数列各项为正,
,且数列各项为正,
故数列为一个递减的等比数列.
故答案为:B
点评:本题考查由数列的递推式来证明数列的特殊性质,属于基础概念题.
解答:解:由于数列{an}满足:a1=1,
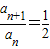 ,
,则数列的后一项为前一项的
 ,且数列各项为正,
,且数列各项为正,故数列为一个递减的等比数列.
故答案为:B
点评:本题考查由数列的递推式来证明数列的特殊性质,属于基础概念题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目