题目内容
（本小题满分25分）已知数列{an}中的相邻两项a2k-1，a2k是关于x的方程x2－（3k+2k）x+3k×2 k =0的两个根.
（1）求数列{an}的前2n项和S2n.
（2）记f（n）=
（
+3），Tn=
+
+
+…+
，
≤Tn≤
（n∈N+）
（I）解析：方程
的两个根为
，
， ………………………………（5分）
． ………………………………（10分）
(Ⅱ) 证明：
，
所以
，
． ………………………………（15分）
当
时，
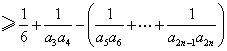
， ………………………………（20分）
同时，
．
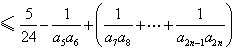
综上，当
时，
． ………………………………（25分）
世纪百通期末金卷系列答案
（2013•宿迁一模）【选做题】本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．（本小题满分12分）一商场对每天进店人数和商品销售件数进行了统计对比，得到如下表格：
|
人数 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
件数 |
4 |
7 |
12 |
15 |
20 |
23 |
27 |
其中
．
（Ⅰ）以每天进店人数为横轴，每天商品销售件数为纵轴，画出散点图；
（Ⅱ）求回归直线方程；（结果保留到小数点后两位）
（参考数据：
，
，
，
，
，
）
（Ⅲ）预测进店人数为80人时，商品销售的件数．（结果保留整数）
（本小题满分12分）
某中学研究性学习小组，为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了 50名学生.调査结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般.
（Ⅰ）试根据以上数据完成以下2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？
高中学生的作文水平与爱看课外书的2×2列联表
|
|
爱看课外书 |
不爱看课外书 |
总计 |
|
作文水平好 |
|
|
|
|
作文水平一般 |
[来源:学。科。网Z。X。X。K] |
|
|
|
总计 |
|
|
|
（Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5，某5名爱看课外书且作文水平一般的学生也分别编号为1、2、3、4、5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
参考公式：
，其中
.
参考数据：
|
|
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
[来源:学*科*网]