题目内容
图1-3-7是一个正方体,H、G、F分别是棱AB、AD、AA1的中点.现在沿三角形GFH所在平面锯掉正方体的一个角,问锯掉的这块的体积是原正方体体积的几分之几?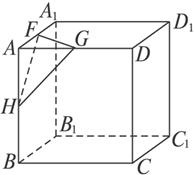
图1-3-7
思路分析:因为锯掉的是立方体的一个角,所以HA与AG、AF都垂直,即HA垂直于三角形AGF所在的立方体的上底面,实际上锯掉的这个角,是以三角形AGF为底面,H为顶点的一个三棱锥.
解:设正方体的棱长为a,则正方体的体积为a3.
三棱锥的底面是直角三角形AGF,而∠FAG为90°,G、F又分别为AD、AA1的中点,
所以AF=AG=![]() a.
a.
这样△AGF的面积为![]() ×
×![]() a×
a×![]() a=
a=![]() a2.AH是三棱锥的高,H又是AB的中点,
a2.AH是三棱锥的高,H又是AB的中点,
所以AH=![]() a.而三棱锥的体积等于底面积与高的乘积再除以3,所以锯掉的那一角的体积为
a.而三棱锥的体积等于底面积与高的乘积再除以3,所以锯掉的那一角的体积为![]() ×
×![]() a×
a×![]() a2=
a2=![]() a3.
a3.
所以锯掉的那块的体积是原正方体体积的![]() .
.
绿色通道:对于三棱锥(或四面体)的体积来说,三棱锥的任何一个面都可以充当它的底面,顶点到这个面的距离即是高.根据题目的已知条件更换底面,可方便地解决相关问题,这种方法在求三棱锥的体积时常用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
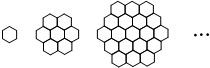 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.


