题目内容
8.(1)若将一粒骰子连续抛掷两次(骰子是有六个面的正方体且每个面分别标有1,2,3,4,5,6)所得到点数分别记为a、b.记“关于x的一元二次方程x2+2ax+b2=0有实根”为事件C.求事件C发生的概率;(2)若a、b均为从区间[0,6]内任取的一个实数,记事件D表示“a2+b2≤16”,求事件D发生的概率.
分析 (1)是古典概型.只要明确事件个数,利用公式解答;
(2)是几何概型,只要求出区域的面积,利用面积比求概率.
解答 解:(1)基本事件总数共6×6=36个…(2分)
事件C共包含21个基本事件,分别为:(1,1)(2,1)(2,2,)(3,1)(3,2)(3,3)(4,1)(4,2)(4,3)(4,4)(5,1)(5,2)(5,3)(5,4)(5,5)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)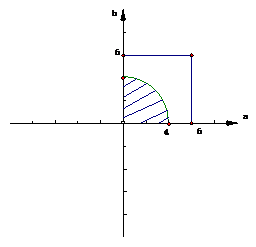
事件C发生的概率P(C)=$\frac{21}{36}=\frac{7}{12}$…(6分)
(2)在如图所示平面直角坐标系下,(a,b)的所有可能结果是边长为6的正方形区域,面积为36,
而事件D“a2+b2≤16”的可能结果由图中阴影部分表示,面积为$\frac{1}{4}π×{4}^{2}=4π$.
由几何概型的概率公式得:
P(D)=$\frac{4π}{36}=\frac{π}{9}$ …(12分)
点评 本题考查了古典概型和几何概型概率的求法;关键是首先明确概率模型,然后根据根式解答.

练习册系列答案
相关题目
19.已知△ABC的三边长分别为a,b,c,若(b+c+a)(b+c-a)=3bc,则角A的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
3.若角α和β的终边关于y轴对称,则下列各式中正确的是( )
| A. | sinα=sinβ | B. | cosα=cosβ | C. | tanα=tanβ | D. | cos(2π-α)=cosβ |
13.已知数列{an}的首项a1=1,an=an-1+3(n≥2,n∈N*),则a4=( )
| A. | 10 | B. | 11 | C. | 9 | D. | 8 |
20.已知过点A(-2,m)和点B(m2,-7)的直线与直线y-1=-2(x+3)平行,则m的值为( )
| A. | $\frac{3}{2}$ | B. | -1 | C. | -1或$\frac{3}{2}$ | D. | 1或-1 |
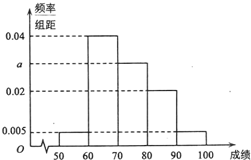 某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 满足
满足 ,则称数列
,则称数列 为调和数列,且
为调和数列,且 ,则
,则 .
.