Question

若关于x的方程k+

x+2

=x有两个不相等的实数解，则实数k的取值范围是

（-

9

4

，-2]

．

Answer 1

分析：原方程化成：

x+2

=x-k，由题意得，直线y=x-k 和曲线 y=

x+2

有两个交点，求出曲线的切线l的斜率，以及过A直线的斜率，即得实数k的取值范围．

解答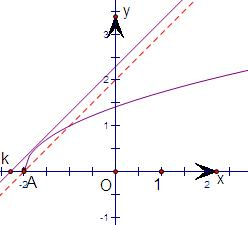：解：关于x的方程：k+

x+2

=x，即

x+2

=x-k，由题意得
直线y=x-k 和 曲线y=

x+2

有两个交点，
如图所示：A（-2，0），
由

x+2

=x-k得x+2=（x-k）²，△=0，∴k=-

9

4

，故曲线的切线l的斜率为-

9

4

．
当直线过A点时，斜率 k=-2，故实数k的取值范围为（-

9

4

，-2]，
故答案为（-

9

4

，-2]．

点评：本题考查根的存在性及根的个数判断，体现了数形结合的数学思想，求出抛物线的切线斜率和过A的直线的斜率是解题的关键．