题目内容
 如图所示,墙上挂有一边长为2的正方形木板,上面画有抛物线型的图案(阴影部分),某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )
如图所示,墙上挂有一边长为2的正方形木板,上面画有抛物线型的图案(阴影部分),某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
开始 |
分析:由题意知本题是一个几何概型,而要求的概率等于阴影部分的面积与正方形的面积之比,题目关键是建立坐标系,写出点的坐标,用定积分来计算阴影部分的面积,最后求比值.
解答:解:以正方形的下面的边为x轴,这边的中点为坐标原点,建立坐标系,
∵(-1,0) (1,0) (0,2)三点在抛物线上,
∴y=-2x2+2,
∴图形中阴影部分的面积S=∫-11(-2x2+2)=[-2
x3+2x]|-11=
,
∵正方形的面积是4,
∴有几何概型概率公式得到P=
=
,
故选C.
∵(-1,0) (1,0) (0,2)三点在抛物线上,
∴y=-2x2+2,
∴图形中阴影部分的面积S=∫-11(-2x2+2)=[-2
| 1 |
| 3 |
| 8 |
| 3 |
∵正方形的面积是4,
∴有几何概型概率公式得到P=
| ||
| 4 |
| 2 |
| 3 |
故选C.
点评:本题考查几何概型和定积分求面积,基本事件不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
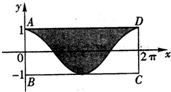 如图所示,墙上挂有一长为2π,宽为2的矩形木板ABCD,它的阴影部分是由函数y=cosx,x∈[0,2π]的图象和直线y=1围成的图形.某人向此板投镖,假设每次都能投中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是
如图所示,墙上挂有一长为2π,宽为2的矩形木板ABCD,它的阴影部分是由函数y=cosx,x∈[0,2π]的图象和直线y=1围成的图形.某人向此板投镖,假设每次都能投中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是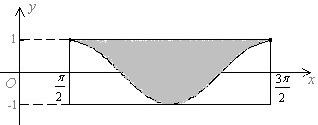 如图所示,墙上挂有一长为2π宽为2的矩形木板ABCD,它的阴影部分是由y=sinx,
如图所示,墙上挂有一长为2π宽为2的矩形木板ABCD,它的阴影部分是由y=sinx, 的图象和直线y=1围成的图形,某人向此板投飞镖,假设每次都能击中木板,且击中木板上每一点的可能性相同,则他击中阴影部分的概率是 .
的图象和直线y=1围成的图形,某人向此板投飞镖,假设每次都能击中木板,且击中木板上每一点的可能性相同,则他击中阴影部分的概率是 .

 的图象和直线y=1围成的图形,某人向此板投飞镖,假设每次都能击中木板,且击中木板上每一点的可能性相同,则他击中阴影部分的概率是 .
的图象和直线y=1围成的图形,某人向此板投飞镖,假设每次都能击中木板,且击中木板上每一点的可能性相同,则他击中阴影部分的概率是 .