题目内容
已知函数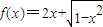
，那么以下的论述中正确的是（ ）A．f（x）有最大值，无最小值
B．f（x）有最小值，无最大值
C．f（x）既有最大值又有最小值
D．f（x）既无最大值也无无最小值
【答案】分析：先求出函数的定义域，然后求出导函数，令导函数为0，求出极值，然后根据导数符号判定函数的单调性，从而求出函数的最值，即可判定选项．
解答：解：函数
的定义域为[-1，1]
f'（x）=2-
令f'（x）=0解得x=
当x∈[-1，
]时，f'（x）＞0，当x∈[
，1]时，f'（x）＜0
而f（-1）=-2，f（1）=2
∴当x=-1时，函数f（x）取最小值-2，当x=
时，函数f（x）取最大值
故选C．
点评：本题主要考查了函数的值域，以及利用导数研究函数的最值，属于中档题．
解答：解：函数
的定义域为[-1，1]f'（x）=2-
令f'（x）=0解得x=
当x∈[-1，
]时，f'（x）＞0，当x∈[，1]时，f'（x）＜0而f（-1）=-2，f（1）=2
∴当x=-1时，函数f（x）取最小值-2，当x=
时，函数f（x）取最大值故选C．
点评：本题主要考查了函数的值域，以及利用导数研究函数的最值，属于中档题．
练习册系列答案
相关题目
已知函数y=f（x）由以下表格表示，那么f（f（1））的值为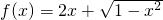
，那么以下的论述中正确的是