题目内容
20.已知a是实数,函数f(x)=2ax2+2x-3-a,如果函数y=f(x)在区间[-1,1]上有零点,求a的取值范围.
解:当a=0时,函数为f (x)=2x -3,其零点x=![]() 不在区间[-1,1]上。
不在区间[-1,1]上。
当a≠0时,函数f (x) 在区间[-1,1]分为两种情况:
①函数在区间[─1,1]上只有一个零点,此时
![]()
或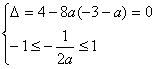
解得1≤a≤5或a=![]()
②函数在区间[─1,1]上有两个零点,此时
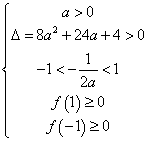 或
或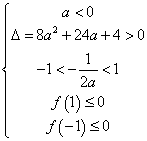
解得a![]() 5或a<
5或a<![]()
综上所述,如果函数在区间[─1,1]上有零点,那么实数a的取值范围为
(-∞,![]() ]∪[1, +∞).
]∪[1, +∞).

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目