题目内容
已知曲线E的参数方程为
|
|
(1)求曲线E和直线l的普通方程.
(2)若点P,Q分别为曲线E,直线l上的动点,求线段PQ长的最小值.
分析:(1)利用同角三角函数的基本关系消去参数θ,把曲线E的参数方程化为普通方程,用代入法消去参数t,
把直线l的参数方程化为普通方程.
(2)设点P(4cosθ,3sinθ),利用点到直线的距离公式可得线段PQ≥
=
,由正弦函数的值域求得其最小值.
把直线l的参数方程化为普通方程.
(2)设点P(4cosθ,3sinθ),利用点到直线的距离公式可得线段PQ≥
| |12cosθ+12sinθ-18| | ||
|
|12
| ||||
| 5 |
解答:解:(1)曲线E的普通方程为
+
=1,直线l的普通方程为 3x+4y-18=0.
(2)设点P(4cosθ,3sinθ),线段PQ≥
=
≥
,故当PQ与直线l垂直,且 θ=2kπ+
,k∈z 时,线段PQ取最小值为
.
| x2 |
| 16 |
| y2 |
| 9 |
(2)设点P(4cosθ,3sinθ),线段PQ≥
| |12cosθ+12sinθ-18| | ||
|
|12
| ||||
| 5 |
18-12
| ||
| 5 |
| π |
| 4 |
18-12
| ||
| 5 |
点评:本题考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,注意线段PQ 取最小值时的条件.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
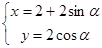 (
(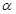 是参数),现以原点O为极点,x轴正半轴为极轴建立极坐标系,
是参数),现以原点O为极点,x轴正半轴为极轴建立极坐标系,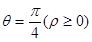 ,曲线C、E相交于A、B两点,求
,曲线C、E相交于A、B两点,求 .
.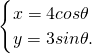 (θ为参数,θ∈R),直线l的参数方程为
(θ为参数,θ∈R),直线l的参数方程为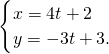 (t为参数,t∈R).
(t为参数,t∈R).