题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,若csinA=acosC,a +b
+b =4(a+b)-8,求c的值。
=4(a+b)-8,求c的值。

解析试题分析:解:由正弦定理得sinCsinA=sinAcosC. 2分
因为0<A<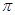 ,所以sinA>0.从而sinC=cosC.
,所以sinA>0.从而sinC=cosC.
又cosC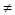 0,所以tanC=1,故C=
0,所以tanC=1,故C= . 5分
. 5分
由a +b
+b =4(a+b)-8,得(a-2)
=4(a+b)-8,得(a-2) +(b-2)
+(b-2) =0,则a=2,b=2. 7分
=0,则a=2,b=2. 7分
又由余弦定理得c =a
=a +b
+b -2abcosC=8-4
-2abcosC=8-4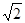 , 9分
, 9分
所以c= . 10分
. 10分
考点:正弦定理和余弦定理
点评:解决的关键是利用三角形的两个定理来进行边角转换求解得到,属于基础题。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 ABC中,
ABC中, 则此三角形的最大边长为
则此三角形的最大边长为  中,已知
中,已知 ,则
,则 ___________.
___________. 中,
中, ,那么A=_____________;
,那么A=_____________; ,则c= .
,则c= . 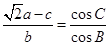 ,则B的大小为 .
,则B的大小为 . 中,内角
中,内角 所对边分别是
所对边分别是 ,已知
,已知 ,
, ,则
,则 中,
中, ,则
,则 的值为___________.
的值为___________. ,则角A的大小为
,则角A的大小为