Question

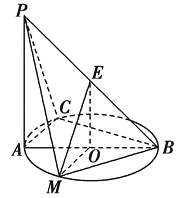
【题目】在四棱椎中，底面为矩形，平面平面， ， ， 为线段上一点，且，点， 分别为线段， 的中点.

(1)求证： 平面；

(2)若平面将四棱椎分成左右两部分，求这两部分的体积之比.

Answer 1

【答案】(1)见解析(2)

【解析】试题分析：（1）证明PE⊥AB，利用平面PAB⊥平面ABCD，即可证明：PE⊥平面ABCD；
（2）若平面EFG将四棱锥P-ABCD分成左右两部分，利用分割法求体积，即可求这两部分的体积之比．

试题解析：

(1)证明：在等腰中， ，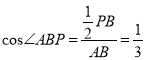

则由余弦定理可得，∴.

∴，∴，

∵平面平面，平面平面，

∴平面.

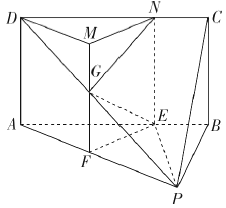
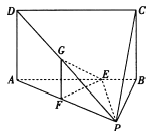
(2)解：设平面与棱交于点，连接，因为，

所以平面，从而可得.

延长至点，使，连接，则为直三棱柱.

∵到的距离为， ，

∴，

∴， ，

∴，

又，

∴.