题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c.已知 .
.
(1)求角B的大小;
(2)设T=sin2A+sin2B+sin2C,求T的取值范围.
解:(1)∵在△ABC中,b2=a2+c2-2accosB,
∴b2-a2-c2=-2accosB,同理可得c2-a2-b2=-2abcosC
∵
∴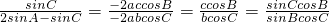 ,…(3分)
,…(3分)
∵sinC≠0,可得sinBcosC=2sinAcosB-sinCcosB,
∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,…(5分)
∵sinA≠0,∴等式两边约去sinA,可得 ,
,
∵0<B<π,∴角B的大小 . …(7分)
. …(7分)
(2)∵B= ,sin2A=
,sin2A= (1-cos2A),sin2C=
(1-cos2A),sin2C= (1-cos2C)
(1-cos2C)
T=sin2A+sin2B+sin2C=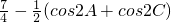
∵A+C= ,可得2C=
,可得2C= -2A,
-2A,
∴cos2A+cos2C=cos2A+cos( -2A)=
-2A)= cos2A-
cos2A- sinA=sin(
sinA=sin( -A)
-A)
因此, =
= -
- sin(
sin( -A)…(11分)
-A)…(11分)
∵ ,可得-
,可得- <
< -A<
-A< ,
,
∴-1≤sin( -A)
-A) ,可得
,可得 ≤
≤ -
- sin(
sin( -A)≤
-A)≤
因此,T=sin2A+sin2B+sin2C的取值范围为[ ,
, ]…(14分)
]…(14分)
分析:(1)根据余弦定理,将题中等式化简整理,可得sinBcosC=2sinAcosB-sinCcosB,称项化简得2sinAcosB=sin(B+C)=sinA,在两边约去sinA得 ,结合三角形内角取值范围即可得到角B的大小;
,结合三角形内角取值范围即可得到角B的大小;
(2)根据B= 代入,结合二倍角的余弦公式降次,再用辅助角公式合并可得T=sin2A+sin2B+sin2C=
代入,结合二倍角的余弦公式降次,再用辅助角公式合并可得T=sin2A+sin2B+sin2C= -
- sin(
sin( -A).最后根据角A的取值范围,结合正弦函数的图象与性质,即可得到T的取值范围.
-A).最后根据角A的取值范围,结合正弦函数的图象与性质,即可得到T的取值范围.
点评:本题在△ABC中给出边角关系式,求角B的大小并求三角正弦的平方和的取值范围.着重考查了利用正余弦定理解三角形、三角恒等变换和三角函数的图象与性质等知识,属于基础题.
∴b2-a2-c2=-2accosB,同理可得c2-a2-b2=-2abcosC
∵

∴
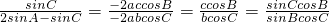 ,…(3分)
,…(3分)∵sinC≠0,可得sinBcosC=2sinAcosB-sinCcosB,
∴2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,…(5分)
∵sinA≠0,∴等式两边约去sinA,可得
 ,
,∵0<B<π,∴角B的大小
 . …(7分)
. …(7分)(2)∵B=
 ,sin2A=
,sin2A= (1-cos2A),sin2C=
(1-cos2A),sin2C= (1-cos2C)
(1-cos2C)T=sin2A+sin2B+sin2C=
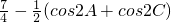
∵A+C=
 ,可得2C=
,可得2C= -2A,
-2A,∴cos2A+cos2C=cos2A+cos(
 -2A)=
-2A)= cos2A-
cos2A- sinA=sin(
sinA=sin( -A)
-A)因此,
 =
= -
- sin(
sin( -A)…(11分)
-A)…(11分)∵
 ,可得-
,可得- <
< -A<
-A< ,
,∴-1≤sin(
 -A)
-A) ,可得
,可得 ≤
≤ -
- sin(
sin( -A)≤
-A)≤
因此,T=sin2A+sin2B+sin2C的取值范围为[
 ,
, ]…(14分)
]…(14分)分析:(1)根据余弦定理,将题中等式化简整理,可得sinBcosC=2sinAcosB-sinCcosB,称项化简得2sinAcosB=sin(B+C)=sinA,在两边约去sinA得
 ,结合三角形内角取值范围即可得到角B的大小;
,结合三角形内角取值范围即可得到角B的大小;(2)根据B=
 代入,结合二倍角的余弦公式降次,再用辅助角公式合并可得T=sin2A+sin2B+sin2C=
代入,结合二倍角的余弦公式降次,再用辅助角公式合并可得T=sin2A+sin2B+sin2C= -
- sin(
sin( -A).最后根据角A的取值范围,结合正弦函数的图象与性质,即可得到T的取值范围.
-A).最后根据角A的取值范围,结合正弦函数的图象与性质,即可得到T的取值范围.点评:本题在△ABC中给出边角关系式,求角B的大小并求三角正弦的平方和的取值范围.着重考查了利用正余弦定理解三角形、三角恒等变换和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |