题目内容
任取实数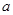 、
、 ,则
,则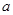 、
、 满足
满足 的概率为( )
的概率为( )
A. | B. | C. | D. |
D
解析试题分析: ,作直线
,作直线 和
和 ,实数
,实数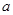 、
、 所满足条件的区域是由四条直线
所满足条件的区域是由四条直线 、
、 、
、 、
、 所围成的正方形区域,而满足条件
所围成的正方形区域,而满足条件 的区域则是正方形区域中夹在两条直线
的区域则是正方形区域中夹在两条直线 和
和 中的部分区域,如下图所示,则事件
中的部分区域,如下图所示,则事件
 所表示的区域为图中的阴影部分所表示的区域,易知直线
所表示的区域为图中的阴影部分所表示的区域,易知直线 分别交直线
分别交直线 与
与 轴于点
轴于点 、
、 ,所以
,所以 ,
, ,所以
,所以 ,易得
,易得
 ,因此
,因此 ,故阴影部分的面积等于
,故阴影部分的面积等于 ,由几何概型的概率公式可知,事件
,由几何概型的概率公式可知,事件 的概率
的概率 ,故选D.
,故选D.
考点:1.线性规划;2.几何概型

练习册系列答案
相关题目
在第3,6,16路公共汽车的一个停靠站(假定这个车站只能停靠一辆公共汽车),有一位乘客需在5分钟之内乘上公共汽车赶到厂里,他可乘3路或6路公共汽车到厂里,已知3路公共汽车、6路公共汽车在5分钟之内到此车站的概率分别为0.20和0.60,则该乘客在5分钟内能乘上所需要的车的概率为( )
| A.0.12 | B.0.20 | C.0.60 | D.0.80 |
从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )
A. | B. | C. | D. |




 表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )













 则射击次数为3的概率为 ( ).
则射击次数为3的概率为 ( ).


