Question

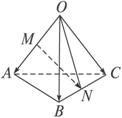
如图,空间四边形OABC中,G,H分别是△ABC,△OBC的重心,设=a,=b,=c,试用向量a,b,c表示向量和.

Answer 1

分析：要用向量a,b,c表示向量，就要找到一组有序实数x,y,z,使=xa+yb+zc,这主要用向量的加法和减法的性质，由向量入手，看一看向量可以由哪些向量的和或差得到.

解：因为=,而=,=,

又因为D是BC的中点,所以=(+).

所以

(a+b+c).

而，

又因为(b+c).

所以=(b+c)-(a+b+c)=-a.

所以=(a+b+c),=-a.

点拨：（1）由于a,b,c三向量不共面，所以｛a,b,c｝构成空间的一个基底，由空间向量基本定理可知空间任一向量均可以由｛a,b,c｝表示.

(2)本题中=()以及=都是常用形式.