题目内容
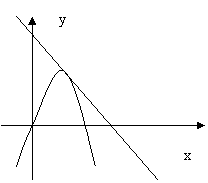 (本题满分16分)开口向下的抛物线
(本题满分16分)开口向下的抛物线![]() 在第一象限内与直线
在第一象限内与直线![]() 相切.此抛物线与
相切.此抛物线与![]() 轴所围成的图形的面积记为
轴所围成的图形的面积记为![]() .
.
(1)求![]() 与
与![]() 的关系式,并用
的关系式,并用![]() 表示
表示![]() 的表达式;
的表达式;
(2)求使![]() 达到最大值的
达到最大值的![]() 、
、![]() 值,并求
值,并求![]()
![]()
解:(1)依题设可知抛物线开口向下,且![]() ,
,
直线x+y=4与抛物线y=ax2+bx相切,即它们有唯一的公共点,
由方程组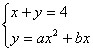 得ax2+(b+1)x-4=0,
得ax2+(b+1)x-4=0,
其判别式必须为0,即(b+1)2+16a=0.
把![]() 代入
代入![]() 得:
得:![]()
(2)![]() ;
;
令S![]() (b)=0;在b>0时得b=3,
(b)=0;在b>0时得b=3,
且当0<b<3时,S![]() (b)>0;当b>3时,S
(b)>0;当b>3时,S![]() (b)<0.
(b)<0.
故在b=3时,S(b)取得极大值,也是最大值,
即a=-1,b=3时,S取得最大值,且![]() 。
。

练习册系列答案
相关题目
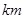 的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?
的圆形村落,A、B两人同时从村落中心O出发,B向北直行,A先向东直行,出村后不久,在点P处改变方向,沿着与村落周界相切的直线前进,后来恰与B在点Q处相遇.设A、B两人速度一定,其速度比为3:1,问Q距O多远?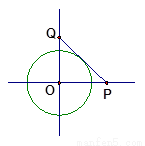
 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.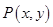 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线 (本题满分16分)开口向下的抛物线
(本题满分16分)开口向下的抛物线