题目内容

已知椭圆E的长轴是短轴的2倍，且经过点（1，0）

   （1）求椭圆E的标准方程；

   （2）若过点M（0，1）的直线l交椭圆E（取焦点在y轴上的椭圆）于点A、B，点P是线段AB的中点，当l绕点M旋转时，求动点P的轨迹方程.

解：（1）设所求椭圆的标准方程为：

由已知得a=2b,且过点（１，０）

   （2）解法一：直线l过点M（0，1）设其斜率为k，则l的方程为

记、由题设可得点A、B的坐标、是方程组

②
 

①
 
                 的解.

将①代入②并化简得，，所以

于是

设点P的坐标为则

消去参数k得     ③

当k不存在时，A、B中点为坐标原点（0，0），也满足方程③，所以点P的轨迹方

程为

解法二：设点P的坐标为，因、在椭圆上，所以

  ④               ⑤

④―⑤得，所以

当时，有      ⑥

并且    ⑦   将⑦代入⑥并整理得     ⑧

当时，点A、B的坐标为（0，2）、（0，－2），

这时点P的坐标为（0，0）也满足⑧，

所以点P的轨迹方程为

练习册系列答案
相关题目
已知椭圆E的方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，长轴是短轴的2倍，且椭圆E过点(
2
，
2
2
)；斜率为k（k＞0）的直线l过点A（0，2），
n
为直线l的一个法向量，坐标平面上的点B满足条件|
n
•
AB
|=|
n
|．
（1）写出椭圆E方程，并求点B到直线l的距离；
（2）若椭圆E上恰好存在3个这样的点B，求k的值．
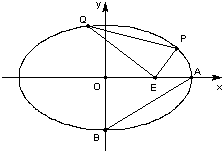精英家教网已知中心在原点O，焦点在x轴上的椭圆C的离心率为
3
2
，点A，B分别是椭圆C的长轴、短轴的端点，点O到直线AB的距离为
6
5
5
．
（1）求椭圆C的标准方程；
（2）已知点E（3，0），设点P、Q是椭圆C上的两个动点，满足EP⊥EQ，求
EP
•
QP
的取值范围．
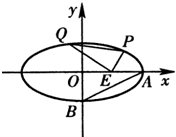精英家教网如图，已知中心在原点O、焦点在x轴上的椭圆C的离心率为
3
2
，点A、B分别是椭圆C的长轴、短轴的端点，点O到直线AB的距离为
6
5
5
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知点E（3，0），设点P、Q是椭圆C上的两个动点，满足EP⊥EQ，求
EP
•
QP
的最小值．
定义：离心率e=
5
-1
2
的椭圆为“黄金椭圆”，已知椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)的一个焦点为F（c，0）（c＞0），P为椭圆E上的任意一点．
（1）试证：若a，b，c不是等比数列，则E一定不是“黄金椭圆”；
（2）没E为黄金椭圆，问：是否存在过点F、P的直线l，使l与y轴的交点R满足
RP
=-2
PF
？若存在，求直线l的斜率k；若不存在，请说明理由；
（3）已知椭圆E的短轴长是2，点S（0，2），求使
SP
2取最大值时点P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网