题目内容
【题目】如图，空间四边形ABCD的对棱AD、BC成600的角，且AD=BC=a，平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H．
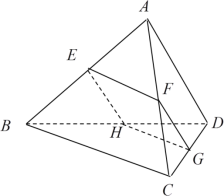
（1）求证：四边形EFGH为平行四边形；
（2）E在AB的何处时截面EFGH的面积最大？最大面积是多少？
【答案】（1）见证明；（2）当E为AB的中点时，截面的面积最大，最大面积为
【解析】
（1）利用线面平行的性质定理证明两组线线平行即可；
（2）设
=x，求出EH=（1﹣x）a．推出S四边形EFGH=EFEHsin60°=．推出E为AB的中点时，截面EFGH的面积最大为．
（１）证明：
平面
，
平面ABC，
平面
平面
，
．同理
，
，同理
，
四边形EGFH为平行四边形．
(2)解：
与BC成
角，
或
设
，
，
，
由
，
得
．
，
，
当
时，，
即当E为AB的中点时，截面的面积最大，最大面积为．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
