题目内容
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)讨论方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
【答案】(1) ![]() ,
, ![]() ;(2)当
;(2)当![]() 时,方程无解;当
时,方程无解;当![]() 或
或![]() 时,方程有唯一解;当
时,方程有唯一解;当![]() 时,方程
时,方程![]() 有两解.
有两解.
【解析】试题分析: (Ⅰ)求出导函数,利用![]() 在处的切线方程为
在处的切线方程为![]() ,列出方程组求解
,列出方程组求解![]() ;(Ⅱ)通过
;(Ⅱ)通过![]() ,判断方程的解
,判断方程的解![]() 出函数的导数判断函数的单调性,求出极小值,分析出当
出函数的导数判断函数的单调性,求出极小值,分析出当![]()
![]() 时,方程无解;当
时,方程无解;当![]() 或
或![]() 时,方程有唯一解;当
时,方程有唯一解;当![]() 时,方程有两解.
时,方程有两解.
试题解析:(Ⅰ)因为![]() ,又
,又![]() 在
在![]() 处得切线方程为
处得切线方程为![]() ,
,
所以![]() ,解得
,解得![]() .
.
(Ⅱ)当![]() 时,
时, ![]() 在定义域
在定义域![]() 内恒大于0,此时方程无解.
内恒大于0,此时方程无解.
当![]() 时,
时, ![]() 在区间
在区间![]() 内恒成立,
内恒成立,
所以![]() 为定义域为增函数,因为
为定义域为增函数,因为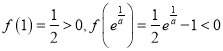 ,
,
所以方程有唯一解.
当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 内为减函数,
内为减函数,
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 内为增函数,
内为增函数,
所以当![]() 时,取得最小值
时,取得最小值![]() .
.
当![]() 时,
时, ![]() ,无方程解;
,无方程解;
当![]() 时,
时, ![]() ,方程有唯一解.
,方程有唯一解.
当![]() 时,
时, ![]() ,
,
因为![]() ,且
,且![]() ,所以方程
,所以方程![]() 在区间
在区间![]() 内有唯一解,
内有唯一解,
当![]() 时,设
时,设![]() ,所以
,所以![]() 在区间
在区间![]() 内为增函数,
内为增函数,
又![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() .
.
因为![]() ,所以
,所以![]() .
.
所以方程![]() 在区间
在区间![]() 内有唯一解,所以方程
内有唯一解,所以方程![]() 在区间
在区间![]() 内有两解,
内有两解,
综上所述,当![]() 时,方程无解.
时,方程无解.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【题目】为了调查喜欢旅游是否与性别有关,调查人员就“是否喜欢旅游”这个问题,在火车站分别随机调研了![]() 名女性或
名女性或![]() 名男性,根据调研结果得到如图所示的等高条形图.
名男性,根据调研结果得到如图所示的等高条形图.

(1)完成下列 ![]() 列联表:
列联表:
喜欢旅游 | 不喜欢旅游 | 估计 | |
女性 | |||
男性 | |||
合计 |
(2)能否在犯错误概率不超过![]() 的前提下认为“喜欢旅游与性别有关”.
的前提下认为“喜欢旅游与性别有关”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
 ,其中
,其中![]()