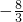Question

若复数z₁=2+mi（m∈R），z₂=4-3i，且

z1

z2

为实数，则m的值为（　　）

• A．

  3

  2

• B．-

  3

  2

• C．-

  8

  3

• D．

  8

  3

Answer 1

分析：根据复数的除法运算首先把复数

z1

z2

化为实部加虚部乘i的形式，然后令虚部为0求m的值．

解答：解：由复数z₁=2+mi（m∈R），z₂=4-3i，
则

z1

z2

=

2+mi

4-3i

=

(2+mi)(4+3i)

(4-3i)(4+3i)

=

(8-3m)+(6+4m)i

25

=

8-3m

25

+

6+4m

25

i，
因为

z1

z2

为实数，所以

6+4m

25

=0，所以m=-

3

2

．
故选B．

点评：本题考查了复数代数形式的乘除运算，考查了复数为实数的充要条件，复数的除法运算是采用分子分母同时乘以分母的共轭复数．