题目内容

设抛物线y²=2px（p＞0）的焦点为F，点A（0，2），若线段FA与抛物线的交点B满足 $数学公式$ ，则点B到该抛物线的准线的距离为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

D
分析：根据抛物线方程可表示出焦点F的坐标，进而求得B点的坐标代入抛物线方程求得p，则B点坐标和抛物线准线方程可求，进而求得B到该抛物线准线的距离．
解答：依题意可知F坐标为（ $\text{[math]}$ ，0）
∴B的坐标为（ $\text{[math]}$ ， $\text{[math]}$ ）代入抛物线方程，解得p= $\text{[math]}$ ，
∴抛物线准线方程为x=- $\text{[math]}$
所以点B到抛物线准线的距离为 $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ，
故选D．
点评：本题主要考查抛物线的定义及几何性质，属容易题．解答的关键是利用方程的思想求出焦参数p．

练习册系列答案

新课程学习与测评高中版系列答案

蓉城学霸系列答案

胜券在握阅读系列答案

新课程实验报告系列答案

新课堂实验报告系列答案

小学生家庭作业系列答案

考易通课时全优练系列答案

与名师对话同步单元测试卷系列答案

黄冈状元笔记系列答案

练习册吉林教育出版集团有限责任公司系列答案

相关题目

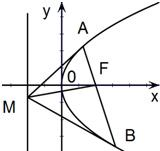设抛物线y²=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A，B两点，且A，B两点坐标分别为（x₁，y₁）、（x₂，y₂），y₁＞0，y₂＜0，M是抛物线的准线上的一点，O是坐标原点．若直线MA，MF，MB的斜率分别记为：K_MA=a，K_MF=b，K_MB=c，（如图）
（I）若y₁y₂=-4，求抛物线的方程；
（II）当b=2时，求a+c的值；
（III）如果取KMA=2，KMB=-

时，判定|∠AMF-∠BMF|和∠MFO的值大小关系．并说明理由．

7、设抛物线y²=2px（p＞0）上一点A（1，2）到点B（x₀，0）的距离等于到直线x=-1的距离，则实数x₀的值是

抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y²=2px（p＞0），弦AB过焦点，△ABQ为阿基米德三角形，则△ABQ为（　　）

A．锐角三角形

B．直角三角形

C．钝角三角形

D．随Q位置变化前三种情况都有可能

设抛物线y²=2px（p＞0）的焦点为F，其准线与x轴的交点为Q，过Q点的直线l交抛物线于A，B两点．
（1）若直线l的斜率为

=0；
（2）设直线FA，FB的斜率分别为k₁，k₂，求k₁+k₂的值．

抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形，阿基米德三角形有一些有趣的性质，如：若抛物线的弦过焦点，则过弦的端点的两条切线的交点在其准线上．设抛物线y²=2px（p＞0），弦AB过焦点，△ABQ为其阿基米德三角形，则△ABQ的面积的最小值为（　　）