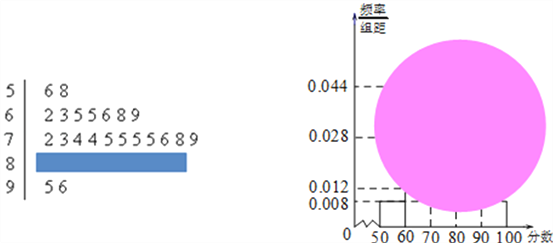
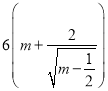题目内容

【题目】如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cos∠B=

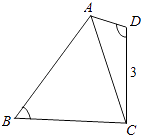
（1）求△ACD的面积；
（2）若BC=2 ，求AB的长．

【答案】
（1）解：因为∠D=2∠B，cos∠B= ，

所以cosD=cos2B=2cos2B﹣1=﹣ ．

因为∠D∈（0，π），

所以sinD= ．

因为 AD=1，CD=3，

所以△ACD的面积S= = = ．


（2）解：在△ACD中，AC2=AD2+DC2﹣2ADDCcosD=12．

所以AC=2 ．

因为BC=2 ， ，

所以 = ．

所以 AB=4．


【解析】（1）利用已知条件求出D角的正弦函数值，然后求△ACD的面积；（2）利用余弦定理求出AC，通过BC=2 ，利用正弦定理求解AB的长．

练习册系列答案
相关题目

【题目】已知定义在R上的函数f（x）= （a∈R）是奇函数，函数g（x）= 的定义域为（﹣1，+∞）．
（1）求a的值；
（2）若g（x）= 在（﹣1，+∞）上递减，根据单调性的定义求实数m的取值范围；
（3）在（2）的条件下，若函数h（x）=f（x）+g（x）在区间（﹣1，1）上有且仅有两个不同的零点，求实数m的取值范围．

【题目】某校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图．

（Ⅰ）求分数在[50，60）的频率及全班人数；

（Ⅱ）求分数在[80，90）之间的频数，并计算频率分布直方图中[80，90）间矩形的高；

（Ⅲ）若要从分数在[80，100）之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在[90，100）之间的概率．

【题目】某市为了了解今年高中毕业生的体能状况，从本市某校高中毕业班中抽取一个班进行铅球测试，成绩在8.0米（精确到0.1米）以上的为合格．把所得数据进行整理后，分成6组画出频率分布直方图的一部分（如图），已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30．第6小组的频数是7．

（1）求这次铅球测试成绩合格的人数；

（2）若由直方图来估计这组数据的中位数，指出它在第几组内，并说明理由；

（3）若参加此次测试的学生中，有9人的成绩为优秀，现在要从成绩优秀的学生中，随机选出2人参加“毕业运动会”，已知a、b的成绩均为优秀，求两人至少有1人入选的概率。

【题目】已知函数f（x）=ln（2+x），g（x）=ln（2﹣x）
（1）判断函数h（x）=f（x）﹣g（x）的奇偶性；
（2）求使f（x）≥g（x）成立的x的取值范围．

【题目】已知函数f（x）=loga（x+1），g（x）=loga（1﹣x）（a＞0且a≠1）．
（1）求f（x）+g（x）的定义域；
（2）判断函数f（x）+g（x）的奇偶性，并证明．

【题目】如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cos∠B=

（1）求△ACD的面积；
（2）若BC=2 ，求AB的长．

【题目】一大学生自主创业，拟生产并销售某电子产品万件（生产量与销售量相等），为扩大影响进行促销，促销费用（万元）满足（其中为正常数）．已知生产该产品还需投入成本万元（不含促销费用），产品的销售价格定为元/件.

（1）将该产品的利润万元表示为促销费用万元的函数；

（2）促销费用投入多少万元时，此大学生所获利润最大？

【题目】已知函数 （p，q为常数）是定义在（﹣1，1）上的奇函数，且 ．
（1）求函数f（x）的解析式；
（2）判断并用定义证明f（x）在（﹣1，1）上的单调性；
（3）解关于x的不等式f（2x﹣1）+f（x）＜0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网