题目内容
已知函数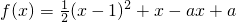 .
.
(I)若 ,求函数f(x)的极值;
,求函数f(x)的极值;
(II)若对任意的x∈(1,3),都有f(x)>0成立,求a取值范围.
解:(I)函数f(x)的定义域为(0,+∞).
f′(x)=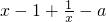 ,
,
当 时,
时,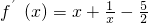 =
=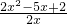 ,
,
令f′(x)=0,解得 或2.列表:
或2.列表:
函数f(x)在 处取得极大值
处取得极大值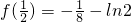 ,
,
函数f(x)在x=2处取得极小值f(2)=ln2- ;
;
(II)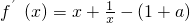 ,当x∈(1,3)时,
,当x∈(1,3)时,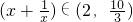 ,
,
(i)当1+a≤2,即a≤1时,x∈(1,3),f′(x)>0,函数f(x)在(1,3)是增函数,
?x∈(1,3),f(x)>f(1)=0恒成立;
(ii)当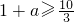 ,即
,即 时,x∈(1,3)时,f′(x)<0,函数f(x)在(1,3)是减函数,
时,x∈(1,3)时,f′(x)<0,函数f(x)在(1,3)是减函数,
?x∈(1,3),f(x)<f(1)=0恒成立,不合题意,应舍去;
(iii)当2<1+a< ,即
,即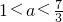 时,x∈(1,3)时,f′(x)先取负,再取0,最后取正,函f(x)在(1,3)先递减,再递增,而f(1)=0,∴?x∈(1,3),f(x)>f(1)=0不能恒成立;
时,x∈(1,3)时,f′(x)先取负,再取0,最后取正,函f(x)在(1,3)先递减,再递增,而f(1)=0,∴?x∈(1,3),f(x)>f(1)=0不能恒成立;
综上,a的取值范围是(-∞,1).
分析:(Ⅰ)先求出函数的导数,利用导数在某点取得极值的条件即可得出;
(Ⅱ)先求导,通过对a分类讨论以确定f′(x)的正负,即函数f(x)的单调性即可得出.
点评:熟练掌握分类讨论的思想方法、利用导数研究函数的单调性等性质是解题的关键.
f′(x)=
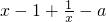 ,
,当
 时,
时,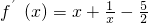 =
=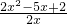 ,
,令f′(x)=0,解得
 或2.列表:
或2.列表:| x |  |  | 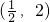 | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 等单调递增 |
 处取得极大值
处取得极大值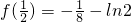 ,
,函数f(x)在x=2处取得极小值f(2)=ln2-
 ;
;(II)
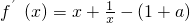 ,当x∈(1,3)时,
,当x∈(1,3)时,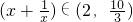 ,
,(i)当1+a≤2,即a≤1时,x∈(1,3),f′(x)>0,函数f(x)在(1,3)是增函数,
?x∈(1,3),f(x)>f(1)=0恒成立;
(ii)当
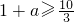 ,即
,即 时,x∈(1,3)时,f′(x)<0,函数f(x)在(1,3)是减函数,
时,x∈(1,3)时,f′(x)<0,函数f(x)在(1,3)是减函数,?x∈(1,3),f(x)<f(1)=0恒成立,不合题意,应舍去;
(iii)当2<1+a<
 ,即
,即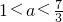 时,x∈(1,3)时,f′(x)先取负,再取0,最后取正,函f(x)在(1,3)先递减,再递增,而f(1)=0,∴?x∈(1,3),f(x)>f(1)=0不能恒成立;
时,x∈(1,3)时,f′(x)先取负,再取0,最后取正,函f(x)在(1,3)先递减,再递增,而f(1)=0,∴?x∈(1,3),f(x)>f(1)=0不能恒成立;综上,a的取值范围是(-∞,1).
分析:(Ⅰ)先求出函数的导数,利用导数在某点取得极值的条件即可得出;
(Ⅱ)先求导,通过对a分类讨论以确定f′(x)的正负,即函数f(x)的单调性即可得出.
点评:熟练掌握分类讨论的思想方法、利用导数研究函数的单调性等性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
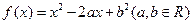 。
。 ,从集合{0,1,2}中任取一个元素作为b,求方程
,从集合{0,1,2}中任取一个元素作为b,求方程 有两个不等实数根的概率;
有两个不等实数根的概率;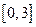 中任取一个数作为
中任取一个数作为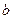 ,求方程
,求方程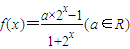 .
.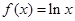 ,
,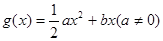
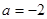 时,函数
时,函数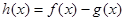 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;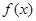 的图象
的图象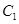 与函数
与函数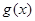 的图象
的图象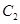 交于点
交于点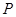 、
、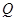 ,过线段
,过线段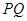 的中点
的中点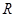 作
作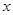 轴的垂线分别交
轴的垂线分别交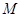 、
、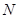 ,问是否存在点
,问是否存在点 .
.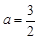 ,求函数
,求函数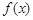 的极值;
的极值;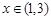 ,都有
,都有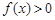 成立,求
成立,求 的取值范围.
的取值范围.