题目内容
已知函数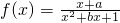 是奇函数,
是奇函数,
(1)求实数a和b的值;
(2)判断函数y=f(x)在(1,+∞)的单调性,并利用定义加以证明.
解:(1)∵f(x)=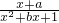 是奇函数,
是奇函数,
∴f(0)=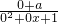 =0,
=0,
∴a=0
又因f(-x)=-f(x),即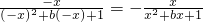 ,
,
∴b=0
(2)函数y=f(x)在(1,+∞)单调递减
证明:任取x1,x2∈(1,+∞),设x1<x2,
则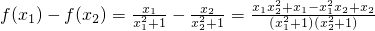
=
∵x1<x2,
∴x1-x2<0;
∵x1>1,x2>1,
∴1-x1x2<0
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2)
函数y=f(x)在(1,+∞)单调递减
分析:(1)由题意可得f(0)=0,从而可求得a,又f(x)是奇函数,可求得b;
(2)由函数单调性的定义判断即可.任取x1,x2∈(1,+∞),设x1<x2,作差f(x1)-f(x2)后化积,判断符号即可.
点评:本题考查函数的奇偶性与单调性的应用,着重考查函数的奇偶性与单调性的定义的应用,突出转化思想的考查,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
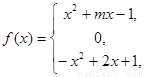
 是奇函数.
是奇函数.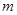 的值;
的值; 在区间
在区间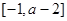 上单调递增,求实数
上单调递增,求实数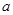 的取值范围;
的取值范围;
 是奇函数.
是奇函数.