Question

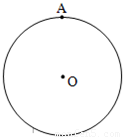
设点A为半径是1的圆O上一定点，在圆周上等可能地任取一点B．

（1）求弦AB的长超过圆内接正三角形边长的概率；

（2）求弦AB的长超过圆半径的概率．

 

Answer 1

【答案】

（1）弦AB的长超过圆内接正三角形边长的概率为．（2）弦AB的长超过圆的半径的概率是．

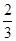【解析】(1) 设“弦AB的长超过圆内接正三角形边长”为事件M，以点A为一顶点，在圆中作一圆内接正三角形ACD，则要满足题意点B只能落在劣弧CD上，又圆内接正三角形ACD恰好将圆周3等分,這樣可得出劣弧CD的長占整個圓周長的.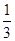

(2) 以圆的半径OA为边长作出两正三角形AOC和AOD，如图所示，

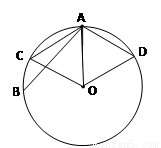
则AC=AD=圆的半径OA，所以满足题意的点B只能落在优弧CD上,然后求出对应的角,从而可求出优弧CD的对应的圆心角,进而得到优弧CD的长,其概率等于.

解：（1）设“弦AB的长超过圆内接正三角形边长”为事件M，以点A为一顶点，在圆中作一圆内接正三角形ACD，如右图所示，

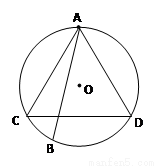
则要满足题意点B只能落在劣弧CD上，又圆内接正三角形ACD恰好将圆周3等分，故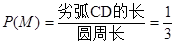．  ……6分

答：弦AB的长超过圆内接正三角形边长的概率为．

（2）设“弦AB的长超过圆的半径”为事件N，

以圆的半径OA为边长作出两正三角形AOC和AOD，如图所示，

则AC=AD=圆的半径OA，所以满足题意的点B只能落在优弧CD上，

又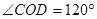，故劣弧CD的长为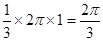，即优弧CD的长为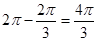

所以．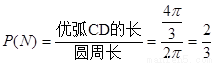

答：弦AB的长超过圆的半径的概率是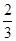．  ……12分