题目内容
【必做题】
已知数列![]() 中,
中,![]() .
.
求证:![]() 对任意
对任意![]() 恒成立.
恒成立.
已知数列![]() 中,
中,![]() .求证:
.求证:![]() 对任意
对任意![]() 恒成立.
恒成立.
证明:(1)当![]() 时,左边=1+1=2,右边=
时,左边=1+1=2,右边=![]() =2,所以命题成立 --------------------2分
=2,所以命题成立 --------------------2分
(2)假设当![]() 时结论成立,即:
时结论成立,即:
![]() -----------------------4分
-----------------------4分
当![]() 时
时
左边=![]() ------------------------- 6分
------------------------- 6分
而![]() ,
,![]()
![]() ,即当
,即当![]() 时结论成立.
时结论成立.
由(1)、(2)可得:命题对于一切![]() 恒成立. --------------------------10分
恒成立. --------------------------10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中有
中有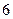 张卡片,其中
张卡片,其中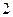 张写有数字
张写有数字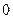 ,
,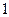 ,
,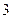 张写有数
张写有数 字
字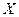 ,求
,求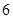 张卡片,其中
张卡片,其中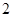 张写有数字
张写有数字 ,
,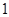 ,
,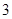 张写有数字
张写有数字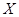 ,求
,求 ,则“海宝”卡至少多少张?
,则“海宝”卡至少多少张? 表示获奖的人数,求
表示获奖的人数,求