题目内容
选做题
如图，AB为圆O的直径，D为圆O上一点，过D作圆O的切线交AB的延长线于点C，若DA=DC，求证：AB=2BC．
如图，AB为圆O的直径，D为圆O上一点，过D作圆O的切线交AB的延长线于点C，若DA=DC，求证：AB=2BC．
解：连接OD，
∵DC是圆O的切线，OD为圆半径，
∴OD⊥DC，
∵DA=DC，
∴∠A=∠C，
设∠A=∠C=α，
∵△ADO中，OA=OD
∴∠ODA=∠A=α，
∴∠ODC=∠ODA+∠A=2α，
∴在Rt△ODC中，∠ODC+∠C=3α=90°，
∴∠C=α=30°
∴Rt△ODC中，OC=2OD=2OB
∴BC=OB=
AB，即AB=2BC．
∵DC是圆O的切线，OD为圆半径，
∴OD⊥DC，
∵DA=DC，
∴∠A=∠C，
设∠A=∠C=α，
∵△ADO中，OA=OD
∴∠ODA=∠A=α，
∴∠ODC=∠ODA+∠A=2α，
∴在Rt△ODC中，∠ODC+∠C=3α=90°，
∴∠C=α=30°
∴Rt△ODC中，OC=2OD=2OB
∴BC=OB=
AB，即AB=2BC．
练习册系列答案
相关题目
,
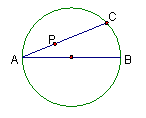动点P的轨迹方程为 ．
,
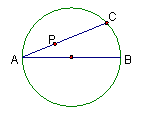动点P的轨迹方程为 ．