题目内容
【题目】如图所示，直线
与椭圆
交于
两点，记
的面积为
（1）当
时，求的最大值；
（2）当
时，求直线
的方程．
【答案】（1）1；（2）
【解析】
（1）利用椭圆的方程求得A，B的横坐标，进而利用弦长公式和b，求得三角形面积表达式，利用基本不等式求得其最大值．
（2）把直线与椭圆方程联立，进而利用弦长公式求得AB的长度的表达式，利用O到直线AB的距离建立方程求得b和k的关系式，求得k．则直线的方程可得．
（1）由题意得，此时
，
将
代入椭圆方程得：
，
，所以，
，
,
当且仅当
，即
时等号成立，所以
的最大值为1.
（2）由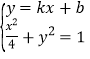
得
（*），其中
，
当
时，设
， 方程（*）两个不等根为
，则有
，
,
,
，①
由
得，
到直线
距离为1，则
，即
，
代入①化简得，
，所以，
，
，经检验，满足，
又因为
，所以
，直线的方程为.
练习册系列答案
相关题目
【题目】已知一个口袋有m个白球，n个黑球（m，n∈N* ， n≥2），这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…，m+n的抽屉内，其中第k次取出的球放入编号为k的抽屉（k=1，2，3，…，m+n）．
1 | 2 | 3 | … | m+n |
（Ⅰ）试求编号为2的抽屉内放的是黑球的概率p；
（Ⅱ）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数，E（X）是X的数学期望，证明E（X）＜ 
．
