题目内容
有定点P(6,4)及定直线l:y=4x,Q是l上在第一象限内的点.PQ交x轴的正半轴于M点,问点Q在什么位置时,△OMQ的面积最小,并求出最小值.分析:设出Q点坐标,写出直线PQ的方程,令x=0求出OM,利用三角形OMQ的OM上的高为Q的纵坐标,则根据三角形的面积公式表示出面积,然后利用基本不等式求出面积的最小值即可.
解答:解:设Q(a,4a),则直线PQ的方程为y-4=
(x-6),
令y=0,得到x=OM=
,
所以当a>1,即a+1>0,a-1>0时,
△OMQ的面积S=
×
×4a=
=10(a+1)+
≥20
当且仅当10(a+1)=
,即a=
时取等号,
所以当Q的坐标为(
,4
)时,面积S的最小值为20
=20
=20(
+1),
| 4-4a |
| 6-a |
令y=0,得到x=OM=
| 5a |
| a-1 |
所以当a>1,即a+1>0,a-1>0时,
△OMQ的面积S=
| 1 |
| 2 |
| 5a |
| a-1 |
| 10a2-10+10 |
| a-1 |
| 10 |
| a-1 |
|
当且仅当10(a+1)=
| 10 |
| a-1 |
| 2 |
所以当Q的坐标为(
| 2 |
| 2 |
|
|
| 2 |
点评:此题为一道中档题,要求学生灵活运用直线的一般式方程求值,灵活运用基本不等式求最值.构造面积的关系式是本题的突破点.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
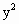 =2px(p>0)上有两动点A、B及一个定点
=2px(p>0)上有两动点A、B及一个定点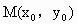 ,F是抛物线的焦点,且|AF|、|MF|、|BF|成等差数列.
,F是抛物线的焦点,且|AF|、|MF|、|BF|成等差数列.