题目内容

在△ABC中，角A，B，C所对的边分别为a、b、c，acosB+bcosA=2ccosC．
（I）求内角C；
（II）若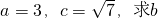 $数学公式$ ．

解：（Ⅰ）∵bcosA+acosB=2ccosC，①
由正弦定理知，b=2RsinB，a=2RsinA，c=2RsinC，②
将②式代入①式，得2sinBcosA+2sinAcosB=4sinCcosC，
化简，得sin（A+B）=sinC=2sinCcosC．

∵sinC≠0，
∴ $\text{[math]}$ ，
∴ $\text{[math]}$ ．
（Ⅱ）∵ $\text{[math]}$ ，
由余弦定理得 $\text{[math]}$
即 $\text{[math]}$ ，
∴ $\text{[math]}$ ．

分析：（1）利用正弦定理将边化成角，再根据和角公式进行化简即可求出角C；
（2）直接利用余弦定理建立关于b的等式关系，解方程即可求出b的值．
点评：本题主要考查了正弦定理与余弦定理的应用，正弦定理、余弦定理是解决有关斜三角形的两个重要定理，属于基础题．

练习册系列答案

新目标课时同步导练系列答案

在△ABC中，角A，B，C所对的边分别为a、b、c，acosB+bcosA=2ccosC．（I）求内角C；（II）若．