Question

若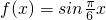，则f（1）+f（3）+f（5）+…+f（2011）=________．

Answer 1

分析：先利用周期公式求出f（x）的周期，且求出一个周期内所有函数值的和，然后用1007除以求出的周期，看余数为几，求出前几项的和即为所求式子的值．
解答：由T=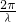==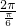12，得到f（x）是以12为周期的函数，
可得：f（1）+f（3）+f（5）+f（7）+f（9）+f（11）=0，
∴f（x）中每连续六项的和等于0，f（x）中共有1007项，
∵1007÷6=167…5，
∴f（x）=f（1）+f（3）+f（5）+f（7）+f（9）
=sinπ6+sin3π6+sin5π6+sin+sin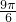
=+1+--1
=．
故答案为：
点评：此题考查了三角函数的周期性及其求法，以及函数的值．求出f（x）的周期且一个周期所有函数值的和是解本题的关键．