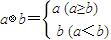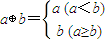Question

对?a，b∈R，定义：max{a，b}=

a，(a≥b) b，(a＜b)

，min{a，b}=

a，(a＜b) b，(a≥b)

．则下列各式：
（1）max{a，b}=

1

2

（a+b-|a-b|）
（2）max{a，b}=

1

2

（a+b+|a-b|）
（3）min{a，b}=

1

2

（a+b+|a-b|）
（4）min{a，b}=

1

2

（a+b-|a-b|）
其中恒成立的是（　　）

A．（1）（2）（3）（4）

B．（1）（2）（3）

C．（1）（3）

D．（2）（4）

Answer 1

∵

1

2

（a+b+|a-b|）=

1 2 (a+b+a-b)，(a≥b) 1 2 (a+b-a+b)，(a＜b)

=

a，(a≥b) b，(a＜b)

=max{a，b}；

1

2

（a+b-|a-b|）=

1 2 (a+b+a-b)，(a＜b) 1 2 (a+b-a+b)，(a≥b)

=

a，(a＜b) b，(a≥b)

=min{a，b}
故选D