题目内容
已知双曲线 与抛物线
与抛物线 有一个公共的焦点
有一个公共的焦点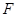 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若 ,则双曲线的渐近线方程为 .
,则双曲线的渐近线方程为 .

解析试题分析:由抛物线y2=8x得出其焦点坐标,由|PF|=5结合抛物线的定义得出点P的坐标,从而得到双曲线 的关于a,b 的方程,求出a,b的值,进而求出双曲线的渐近线方程。解:抛物线y2=8x得出其焦点坐标(2,0)故双曲线的c=2,又|PF|=5,设P(m,n),则|PF|=m+2∴m+2=5,m=3,∴点P的坐标(3,±
的关于a,b 的方程,求出a,b的值,进而求出双曲线的渐近线方程。解:抛物线y2=8x得出其焦点坐标(2,0)故双曲线的c=2,又|PF|=5,设P(m,n),则|PF|=m+2∴m+2=5,m=3,∴点P的坐标(3,± )∴a 2+b 2=4,
)∴a 2+b 2=4, 解得:a 2=1,b 2=3则双曲线的渐近线方程为
解得:a 2=1,b 2=3则双曲线的渐近线方程为 故答案为
故答案为 。
。
考点:抛物线的简单性质,双曲线的简单性质
点评:本题主要考查了抛物线的简单性质,双曲线的简单性质,抛物线的定义等.解答的关键是学生对圆锥曲线基础知识掌握的熟练程度.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 :
: 上有一点
上有一点 ,若它到点
,若它到点 的距离与它到抛物线
的距离与它到抛物线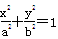 (a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=
(a>b>0)的左,右焦点,点P是椭圆在y轴右侧上的点,且∠F1PF2=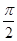 ,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1∶2,则该椭圆的离心率等于
,记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1∶2,则该椭圆的离心率等于  ,则抛物线的标准方程是_________。
,则抛物线的标准方程是_________。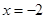 ,则抛物线的标准方程是______________。
,则抛物线的标准方程是______________。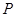 在曲线
在曲线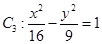 上,点Q在曲线
上,点Q在曲线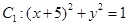 上,点R在曲线
上,点R在曲线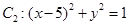 上,则
上,则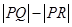 最大值是
最大值是  ,曲线
,曲线 :
: 上的点到直线的距离为
上的点到直线的距离为 ,则
,则 的准线方程是x=1;
的准线方程是x=1;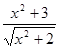 的最小值是2;
的最小值是2; ;
; )且P(0≤ξ≤3)=0.4,则P(ξ≥6)=0.1 。
)且P(0≤ξ≤3)=0.4,则P(ξ≥6)=0.1 。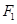 ,
,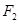 ,且它们在第一象限的交点为P,△
,且它们在第一象限的交点为P,△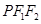 是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若