题目内容
定义在R上的偶函数满足：对任意x1，x2∈[0，+∞），且x1≠x2都有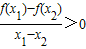
，则（ ）A．f（3）＜f（-2）＜f（1）
B．f（1）＜f（-2）＜f（3）
C．f（-2）＜f（1）＜f（3）
D．f（3）＜f（1）＜f（-2）
【答案】分析：先根据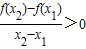 
判断出（x2-x1）（f（x2）-f（x1））＞0，进而可推断f（x）在x1，x2∈[0，+∞）（x1≠x2）上单调递增，又由于f（x）是偶函数，可知在x1，x2∈（-∞，0]（x1≠x2）单调递增．进而可判断出f（3），f（-2）和f（1）的大小．
解答：解：∵（x2-x1）（f（x2）-f（x1））＞0，
∴
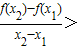则f（x）在x1，x2∈[0，+∞）（x1≠x2）上单调递增，
又f（x）是偶函数，故f（x）在x1，x2∈（-∞，0]（x1≠x2）单调递减．
且满足n∈N*时，f（-2）=f（2），3＞2＞1＞0，
得f（1）＜f（-2）＜f（3），
故选B．
点评：本题主要考查了函数奇偶性的应用和函数的单调性的应用．属基础题．
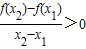判断出（x2-x1）（f（x2）-f（x1））＞0，进而可推断f（x）在x1，x2∈[0，+∞）（x1≠x2）上单调递增，又由于f（x）是偶函数，可知在x1，x2∈（-∞，0]（x1≠x2）单调递增．进而可判断出f（3），f（-2）和f（1）的大小．解答：解：∵（x2-x1）（f（x2）-f（x1））＞0，
∴
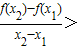则f（x）在x1，x2∈[0，+∞）（x1≠x2）上单调递增，又f（x）是偶函数，故f（x）在x1，x2∈（-∞，0]（x1≠x2）单调递减．
且满足n∈N*时，f（-2）=f（2），3＞2＞1＞0，
得f（1）＜f（-2）＜f（3），
故选B．
点评：本题主要考查了函数奇偶性的应用和函数的单调性的应用．属基础题．
练习册系列答案
相关题目
定义在R上的偶函数f（x），满足以f（x+2）=-f（x）且在[0，2]上是减函数，若方程f（x）=m（m＞0）在区间[-2，6]上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4= ．
定义在R上的偶函数f（x），满足以f（x+2）=-f（x）且在[0，2]上是减函数，若方程f（x）=m（m＞0）在区间[-2，6]上有四个不同的根x1，x2，x3，x4，则x1+x2+x3+x4= ．