题目内容
点O是三角形ABC所在平面内的一点,满足(| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
分析:由
•
=
•
得到 (
)•(
)=0,根据向量数量积为零可得OB⊥AC,同理得到OA⊥BC,所以点O是△ABC的三条高的交点,从而根据垂心的定义可得结论.
| OA |
| OB |
| OB |
| OC |
| OB |
| CA |
解答:解:(
)•(
)=(
)•(
),
(
)•(
)-(
)•(
)=0,
即(
)•(
)-(
))=0,
(
)•(
)=0,
∴(
)⊥(
).
同理可得(
)⊥(
),(
)⊥(
).
∴O是三角形三条高线的交点.
故答案为:垂
| OA |
| OB |
| OB |
| OC |
(
| OB |
| OA |
| OB |
| OC |
即(
| OB |
| OA |
| OC |
(
| OB |
| CA |
∴(
| OB |
| CA |
同理可得(
| OA |
| BC |
| OC |
| AB |
∴O是三角形三条高线的交点.
故答案为:垂
点评:本题考查向量的数量积及向量的运算,对学生有一定的能力要求,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
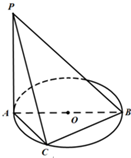 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.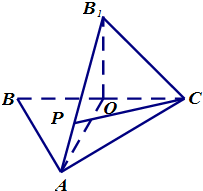 (2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
(2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.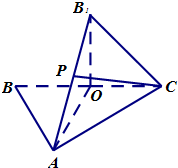 (2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
(2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
 是直径
是直径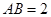 的圆上一点,
的圆上一点,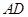 为圆O的切线,
为圆O的切线,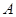 为切点,
为切点,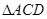 为等边三角形,连接
为等边三角形,连接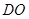 交
交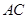 于
于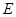 ,以
,以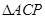 的位置,点P为平面ABC外的点.
的位置,点P为平面ABC外的点.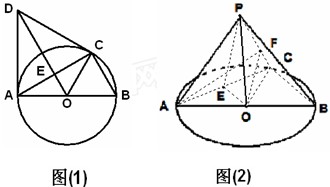
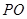 互相垂直;
互相垂直;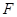 为
为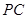 上一点,且
上一点,且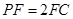 ,
,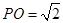 ,求三棱锥
,求三棱锥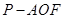 的体积.
的体积.