题目内容

设f（x）是定义是R上恒不为零的函数，对任意x，y∈R，都有f（x）·f（y）＝f（x＋y）,若a₁＝，a_n＝f（n）(n为正整数)，则数列{ a_n }的前n项和S_n的取值范围是（）

A. ≤S_n＜2 B. ≤S_n≤2 C. ≤S_n≤1 D. ≤S_n＜1

D

解析:

由条件得：f（n）·f（1）＝f（n＋1），即a_n+1＝a_n·，得数列{ a_n }是首项与公比均为的等比数列，求和得S_n＝1－（）ⁿ，得选D .

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

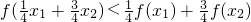设f（x）是定义在集合D上的函数，若对集合D中的任意两数x₁，x₂恒有 $数学公式$ 成立，则f（x）是定义在D上的β函数．
（1）试判断f（x）=x²是否是其定义域上的β函数？
（2）设f（x）是定义在R上的奇函数，求证：f（x）不是定义在R上的β函数．
（3）设f（x）是定义在集合D上的函数，若对任意实数α∈[0，1]以及集合D中的任意两数x₁，x₂恒有f（αx₁+（1-α）x₂）≤αf（x₁）+（1-α）f（x₂），则称f（x）是定义在D上的α-β函数．已知f（x）是定义在R上的α-β函数，m是给定的正整数，设a_n=f（n），n=1，2，3…m且a₀=0，a_m=2m，记∫=a₁+a₂+a₃+…+a_m，对任意满足条件的函数f（x），求∫的最大值．

设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）

设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）

设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）