Question

（本小题满分12分）

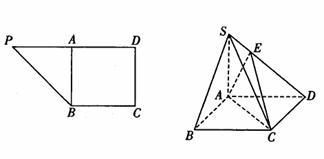
    在直角梯形中，，为的中点，如下左图.将沿折到的位置，使，点在上，且，如下右图.

   （1）求证：平面；

   （2）求二面角的正切值；

   （3）在线段上是否存在点，使平面？若存在，确定的位置，若不存在，请说明理由.

Answer 1

【解】【解法一】（1）证明：在上左图中，由题意可知，为正方形，

所以在上右图中，，四边形是边长为2的正方形，

因为，，所以平面SAB，

又平面SAB，所以BCSA，又SAAB，

所以SA平面ABCD.        4分

 （2）在AD上取一点O，使，连接EO.因为，所以

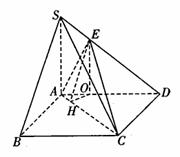EO//SA所以EO平面ABCD，过O作OHAC交AC于H，连接EH，则AC平面EOH，所以ACEH.所以为二面角E—AC—D的平面角，在中，

_{即二面角E—AC—D的正切值为}       12分

（3）当F为BC中点时，SF//平面EAC，理由如下：取BC的中点F，连接DF交AC于M，连接EM，AD//FC，所以,又由题意，SF//EM，又平面EAC，所以SF//平面EAC，即当F为BC的中点时，SF//平面EAC      12分

【解法二】（1）同解法一    4分

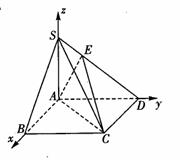
（2）如图，以A为原点建立直角坐标系，A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），S（0，0，2），E（0，）易知平面ACD的法向为设平面EAC的法向量为

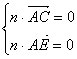由，所以，

可取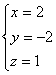_，所以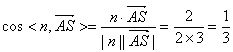

所以，所以，

即二面角E—AC—D的正切值为     8分

（3）设存在，所以SF//平面EAC，设所以，由SF//平面EAC，所以，所以0，即，

即F（2，1，0）为BC的中点。       12分