题目内容
已知函数f(x)=
x3-x2+3,x∈[-1,t](t>-1).
(Ⅰ)当t=3时,求函数f(x)的单调区间和最值;
(Ⅱ)设函数g(t)=
(t-2)2,t>-1.记方程f'(x)=g(t)的解为x0,x0∈(-1,t),就t的取值情况讨论x0的个数.
| 1 |
| 3 |
(Ⅰ)当t=3时,求函数f(x)的单调区间和最值;
(Ⅱ)设函数g(t)=
| 1 |
| 3 |
分析:(Ⅰ)由题意,对函数求导得到f'(x)=x2-2x=x(x-2),可得出当t=3时,f(x)在(-1,0),(2,3)上递增,在(0,2)上递减,由此函数的最值与单调区间易求得;
(II)解法一:由题意函数g(t)=
(t-2)2,t>-1.记方程f'(x)=g(t),可得出x2-2x=
(t-2)2,由于方程f'(x)=g(t)的解为x0,x0∈(-1,t),故可构造函数p(x)=x2-2x-
(t-2)2在x0∈(-1,t),分类讨论x0的个数;
解法二:可作出两函数f'(x)=x2-2x与g(t)=
(t-2)2,t>-1的图象,由图象对t的取值范围分类讨论得出每一种情况下两个函数图象的交点个数即可得到x0的个数.
(II)解法一:由题意函数g(t)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解法二:可作出两函数f'(x)=x2-2x与g(t)=
| 1 |
| 3 |
解答:解:(Ⅰ)因为f'(x)=x2-2x=x(x-2)…(1分)
由f'(x)>0⇒x>2或x<0;由f'(x)<0⇒0<x<2,
所以当t=3时,f(x)在(-1,0),(2,3)上递增,在(0,2)上递减 …(3分)
因为f(-1)=
,f(0)=3,f(2)=
-4+3=
,f(3)=3,
所以当x=-1或2时,函数f(x)取最小值f(-1)=
,…(5分)
当x=0或3时,函数f(x)取最大值f(0)=3,…(6分)
(Ⅱ)解法1:因为f'(x)=x2-2x,所以x2-2x=
(t-2)2,
令p(x)=x2-2x-
(t-2)2,
因为p(-1)=3-
(t-2)2=-
(t+1)(t-5),p(t)=t(t-2)-
(t-2)2=
(t+1)(t-2),…(9分)
所以①当t>5或-1<t<2时,p(-2)•p(t)<0,所以p(x)=0在(-2,t)上有且只有一解…(11分)
②当2<t<5时,p(-2)>0且p(t)>0,但由于p(0)=-
(t-2)2<0,
所以p(x)=0在(-2,t)上有两解 …(13分)
③当t=2时,p(x)=x2-2x=0⇒x=0或x=2,所以p(x)=0在(-2,t)上有且只有一解x=0;
当t=5时,p(x)=x2-2x-3=0⇒x=-1或x=3,
所以p(x)=0在(-1,5)上也有且只有一解x=3…(14分)
综上所述,当t≥5或-1<t≤2时,有唯一的x0适合题意;当2<t<5时,有两个x0适合题意.…(15分)
解法2:画出f'(x)=x2-2x与g(t)=
(t-2)2,t>-1的图象,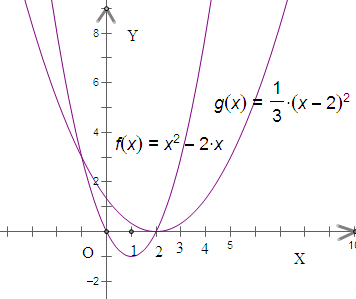
(1)当-1<t≤0时,两图象有一个交点,有唯一的x0适合题意;-------------(8分)
(2)当0<t≤2时,0≤
(t-2)2<
,此时两图象有一个交点,有唯一的x0适合题意;-------------(10分)
(3)当2<t<5时,因为f'(-1)=f'(3)=3,
(t-2)2=3得到t1=-1,t2=5,0<
(t-2)2<3,此时两图象有两个交点,有两个x0适合题意;------(12分)
(4)当t=2或t=5时,当t=2时,p(x)=x2-2x=0⇒x=0或x=2,所以p(x)=0在(-2,t)上有且只有一解x=0;
当t=5时,p(x)=x2-2x-3=0⇒x=-1或x=30<
(t-2)2<3,
此时两图象有两个交点,有两个x0适合题意;---------------------(14分)
综上所述,当t≥5或-1<t≤2时,有唯一的x0适合题意;
当2<t<5时,有两个x0适合题意.…(15分)
由f'(x)>0⇒x>2或x<0;由f'(x)<0⇒0<x<2,
所以当t=3时,f(x)在(-1,0),(2,3)上递增,在(0,2)上递减 …(3分)
因为f(-1)=
| 5 |
| 3 |
| 8 |
| 3 |
| 5 |
| 3 |
所以当x=-1或2时,函数f(x)取最小值f(-1)=
| 5 |
| 3 |
当x=0或3时,函数f(x)取最大值f(0)=3,…(6分)
(Ⅱ)解法1:因为f'(x)=x2-2x,所以x2-2x=
| 1 |
| 3 |
令p(x)=x2-2x-
| 1 |
| 3 |
因为p(-1)=3-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
所以①当t>5或-1<t<2时,p(-2)•p(t)<0,所以p(x)=0在(-2,t)上有且只有一解…(11分)
②当2<t<5时,p(-2)>0且p(t)>0,但由于p(0)=-
| 1 |
| 3 |
所以p(x)=0在(-2,t)上有两解 …(13分)
③当t=2时,p(x)=x2-2x=0⇒x=0或x=2,所以p(x)=0在(-2,t)上有且只有一解x=0;
当t=5时,p(x)=x2-2x-3=0⇒x=-1或x=3,
所以p(x)=0在(-1,5)上也有且只有一解x=3…(14分)
综上所述,当t≥5或-1<t≤2时,有唯一的x0适合题意;当2<t<5时,有两个x0适合题意.…(15分)
解法2:画出f'(x)=x2-2x与g(t)=
| 1 |
| 3 |
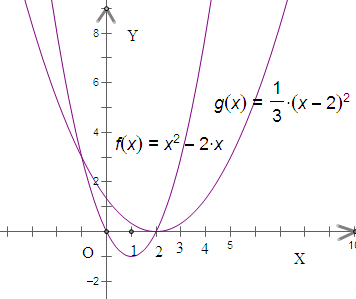
(1)当-1<t≤0时,两图象有一个交点,有唯一的x0适合题意;-------------(8分)
(2)当0<t≤2时,0≤
| 1 |
| 3 |
| 4 |
| 3 |
(3)当2<t<5时,因为f'(-1)=f'(3)=3,
| 1 |
| 3 |
| 1 |
| 3 |
(4)当t=2或t=5时,当t=2时,p(x)=x2-2x=0⇒x=0或x=2,所以p(x)=0在(-2,t)上有且只有一解x=0;
当t=5时,p(x)=x2-2x-3=0⇒x=-1或x=30<
| 1 |
| 3 |
此时两图象有两个交点,有两个x0适合题意;---------------------(14分)
综上所述,当t≥5或-1<t≤2时,有唯一的x0适合题意;
当2<t<5时,有两个x0适合题意.…(15分)
点评:本题考查导数在最值问题中的应用,考查了求导的运算,由导数求函数的单调区间,方程的交点个数与方程相应函数的交点的对应关系解题的关键是理解题意灵活利用导数的知识求最值,研究单调性,本题解题的难点在第二小题,由于t的取值范围不同,方程的根的个数不同,故采取了分类讨论的方法,本题考查了分类讨论的思想,转化的思想,及推理判断的能力,计算能力,本题综合性强,运算量大,易出错,做题时要严谨.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目