题目内容
(本小题满分12分)
已知半椭圆![]() 和半圆
和半圆![]()
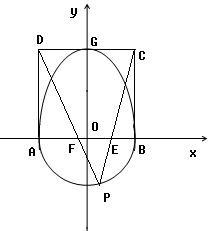 组成曲线
组成曲线![]() ,其中
,其中![]() ;如图,半椭圆
;如图,半椭圆
![]() 内切于矩形
内切于矩形![]() ,
,
且![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是半圆
是半圆![]() 上
上
异于![]() 的任意一点,当点
的任意一点,当点![]() 位于点
位于点![]() 时,
时,
![]() 的面积最大.
的面积最大.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)连![]() 、
、![]() 交
交![]() 分别于点
分别于点![]() ,求证:
,求证:![]() 为定值.
为定值.
解:(Ⅰ)已知点![]() 在半圆
在半圆![]() 上,
上,
所以![]() ,又
,又![]() ,所以
,所以![]() , ………………(2分)
, ………………(2分)
当半圆![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行时,点
平行时,点![]() 到直线
到直线![]() 的距离最大,此时
的距离最大,此时![]() 的面积取得最大值,
的面积取得最大值,
故半圆![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,
平行,
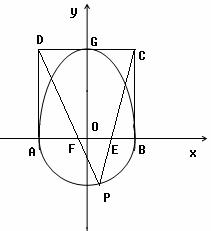 所以
所以![]() ,又
,又![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() , ………………(4分)
, ………………(4分)
所以曲线![]() 的方程为
的方程为
![]() 或
或![]() 。…………(5分)
。…………(5分)
(Ⅱ)点![]() ,点
,点![]() ,设
,设![]() ,则有
,则有
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得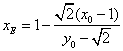 ,
,
所以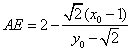 ; ………………(7分)
; ………………(7分)
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得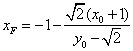 ,
,
所以 ; ………………(9分)
; ………………(9分)
则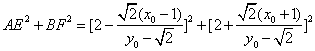
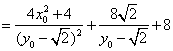 , ………………(10分)
, ………………(10分)
又由![]() ,得
,得![]() ,代入上式得
,代入上式得
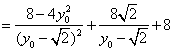
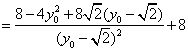
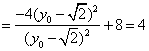 ,所以
,所以![]() 为定值。 ………………(12分)
为定值。 ………………(12分)

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目