题目内容
在平面直角坐标系xOy中,△ABC的顶点B、C的坐标为B(-2,0),C(2,0),直线AB,AC的斜率乘积为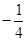 ,设顶点A的轨迹为曲线E.
,设顶点A的轨迹为曲线E.
(1)求曲线E的方程;
(2)设曲线E与y轴负半轴的交点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与曲线E的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,试求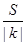 的取值范围.
的取值范围.
(1) ;(2)
;(2)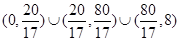
解析试题分析:(1)由于所求动点A满足直线AB,AC的斜率乘积为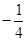 ,所以直接设A的坐标,代入化简整理即得:
,所以直接设A的坐标,代入化简整理即得: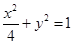 ,注意到△ABC中三个顶点不能共线,所以需去掉与
,注意到△ABC中三个顶点不能共线,所以需去掉与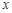 轴相交的点,(2)要求
轴相交的点,(2)要求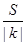 的取值范围,首先求出
的取值范围,首先求出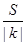 函数解析式,由题意确定l1的斜率为k为自变量,因为M 为l1与曲线E的交点,所以列方程组解出点M坐标
函数解析式,由题意确定l1的斜率为k为自变量,因为M 为l1与曲线E的交点,所以列方程组解出点M坐标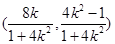 ,从而得出弦长
,从而得出弦长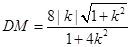 ;同理,只需将
;同理,只需将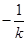 代k就可得到
代k就可得到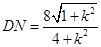 ,因此△DMN的面积S=
,因此△DMN的面积S=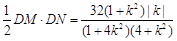 ,所以
,所以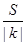 =
= ,这可以看作关于1+k2的一个分式函数,即
,这可以看作关于1+k2的一个分式函数,即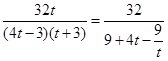 ,可以利用函数单调性求出其取值范围.
,可以利用函数单调性求出其取值范围.
试题解析:解(1)设顶点A的坐标为(x,y),则kAB=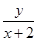 ,kAC=
,kAC=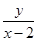 2分
2分
因为kAB×kAC=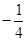 ,所以
,所以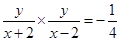 , 即
, 即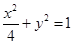 .(或x2+4y2=4).
.(或x2+4y2=4).
所以曲线E的方程为 . 4分
. 4分
(2)曲线E与y轴负半轴的交点为D(0,-1).
因为l1的斜率存在,所以设l1的方程为y=kx-1, 代入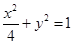 ,得
,得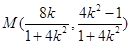
从而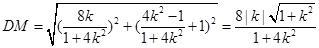 6分
6分
用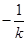 代k得
代k得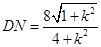
所以△DMN的面积S=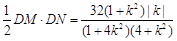 8分
8分
则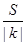 =
= 
因为k≠0且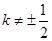 ,k≠±2,令1+k2=t,
,k≠±2,令1+k2=t,
则t>1,且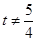 ,t≠5,
,t≠5,
从而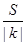 =
= 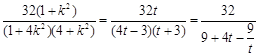
因为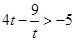 ,且
,且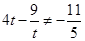 ,
,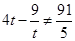
所以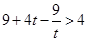 且
且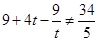 ,
,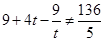
从而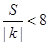 且
且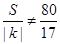 ,
,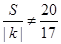 ,
,
即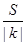 ∈
∈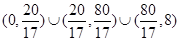 10分.
10分.
考点:直接法求轨迹方程,直线与圆锥曲线关系,求函数范围

练习册系列答案
相关题目
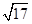 ,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.
 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,连结椭圆的四个顶点得到的菱形的面积为4.
,连结椭圆的四个顶点得到的菱形的面积为4. ,求直线l的倾斜角.
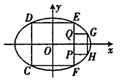
,求直线l的倾斜角.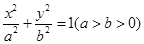 ,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=
,且它的四条边与坐标轴平行,正方形GHPQ的顶点G,H在椭圆上,顶点P,Q在正方形的边EF上.且CD=2PQ=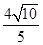 .
.
 +
+ =1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
=1(a>b>0)的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
 ,
, ),Q(
),Q(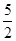 ,1),求椭圆C1的方程;
,1),求椭圆C1的方程; +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.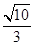 时,求k的值.
时,求k的值. =1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2
=1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2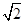 ,|AB|的最小值为2.
,|AB|的最小值为2.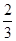 的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.