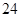题目内容
已知 为常数,若曲线
为常数,若曲线 存在与直线
存在与直线 垂直的切线,则实数
垂直的切线,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析:因为直线x+y-1=0直线的斜率为-1,那么所求的曲线的切线的斜率为1,故设切点为(m,n),则因为f’(x)=2ax+3- =1方程有解,同时要助于定义域x>0,那么分离参数2ax=
=1方程有解,同时要助于定义域x>0,那么分离参数2ax= -2,可得a=
-2,可得a= (x>0),求解右边函数的值域即为参数a的范围。则根据
(x>0),求解右边函数的值域即为参数a的范围。则根据 ,结合二次函数的性质可知其范围是a
,结合二次函数的性质可知其范围是a ,故选A.
,故选A.
考点:本题主要考查了导数的几何意义的运用。
点评:解决该试题的关键是利用两条直线的垂直关系,得到切线的斜率值,然后利用导数的几何意义,得到该点的导数值。进而方程有解得到a的范围。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
若直线 与直线
与直线 垂直,则
垂直,则 的值为 ( )
的值为 ( )
| A.2 | B.-3或1 | C.2或0 | D.1或0 |
已知直线 与曲线
与曲线 在点
在点 处的切线互相垂直,则
处的切线互相垂直,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知直线 方程为
方程为 ,且在
,且在 轴上的截距为
轴上的截距为 ,在
,在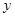 轴上的截距为
轴上的截距为 ,则
,则 等于( )
等于( )
| A.3 | B.7 | C.10 | D.5 |
已知过点 和
和 的直线与直线
的直线与直线 平行,则
平行,则 的值为( ).
的值为( ).
A. | B. | C. | D. |
过点(1,0)且与直线x-2y-2=0平行的直线方程是( )
| A.x-2y-1=0 | B.x-2y+1="0" | C.2x+y-2=0 | D.x+2y-1=0 |
直线 (
( 为实常数)的倾斜角的大小是 ( )
为实常数)的倾斜角的大小是 ( )
A. | B. | C. | D. |
已知直线 ,函数
,函数 的图象与直线
的图象与直线 相切于P点,若
相切于P点,若 ,则P点的坐标可能是( )
,则P点的坐标可能是( )
A. | B.  | C. | D. |
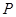 在直线
在直线 上
上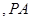 、
、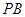 与圆
与圆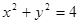 分别相切于
分别相切于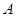 、
、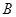 两点
两点 则四边形
则四边形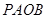 的面积的最小值为( )
的面积的最小值为( )