题目内容

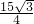在△ABC中，角A，B，C所对应的边分别是a，b，c，已知（b+c）：（c+a）：（a+b）=4：5：6，给出下列结论①△ABC的边长可以组成等差数列 $数学公式$ $数学公式$ ④若b+c=8，则△ABC的面积是 $数学公式$ 其中正确的结论序号是________．

①②④
分析：由已知可设b+c=4k，c+a=5k，a+b=6k（k＞0），然后分别求出a、b、c的值，即可判断2b与a+c相等得到三边成等差数列，利用余弦定理求出角A的余弦值即可判定A为钝角，利用平面向量的数量积得运算法则求出 $\text{[math]}$ • $\text{[math]}$ 的值，并根据面积公式即可求出三角形ABC的面积，再与题目进行比较即可．
解答：由已知可设b+c=4k，c+a=5k，a+b=6k（k＞0），
则a= $\text{[math]}$ k，b= $\text{[math]}$ k，c= $\text{[math]}$ k，
∴a：b：c=7：5：3，∴2b=a+c，
即△ABC的边长可以组成等差数列，故①正确；
∴sinA：sinB：sinC=7：5：3，故③错误；
又cosA= $\text{[math]}$ =- $\text{[math]}$ ＜0，
∴△ABC为钝角三角形，∴ $\text{[math]}$ • $\text{[math]}$ =bccosA＜0，故②正确；
若b+c=8，则k=2，∴b=5，c=3，
又A=120°，∴S_△ABC= $\text{[math]}$ bcsinA= $\text{[math]}$ $\text{[math]}$ ，故④正确；
所以正确的结论序号是：①②④．
故答案：①②④
点评：本题主要考查了正弦定理以及余弦定理的运用，利用三角形的面积公式求解面积，属于基础题．