题目内容
若直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则 +
+ 的最小值为( )
的最小值为( )
(A) (B)
(B)
(C) +
+ (D)
(D) +2
+2
【答案】
C
【解析】圆的标准方程为(x+1)2+(y-2)2=4,
所以圆心坐标为(-1,2),半径为r=2.
因为直线被圆截得的弦长为4,
所以直线ax-by+2=0过圆心,
所以-a-2b+2=0,
即a+2b=2,
所以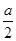 +b=1,
+b=1,
所以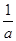 +
+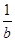 =(
=(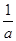 +
+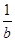 )(
)(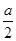 +b)
+b)
=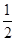 +1+
+1+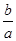 +
+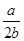
≥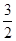 +2
+2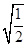
=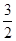 +
+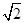 .
.
当且仅当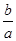 =
=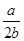 ,a=
,a=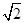 b时取等号,
b时取等号,
所以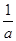 +
+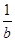 的最小值为
的最小值为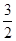 +
+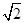 .故选C.
.故选C.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若直线ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|