题目内容
11.若函数y=sin(ωx+$\frac{5π}{3}$)(ω>0)的最小正周期是$\frac{π}{3}$,则ω=6.分析 由条件根据函数y=Asin(ωx+φ)的周期为 $\frac{2π}{ω}$,可得结论.
解答 解:函数y=sin(ωx+$\frac{5π}{3}$)(ω>0)的最小正周期是$\frac{2π}{ω}$=$\frac{π}{3}$,则ω=6,
故答案为:6.
点评 本题主要考查函数y=Asin(ωx+φ)的周期性,利用了函数y=Asin(ωx+φ)的周期为 $\frac{2π}{ω}$,属于基础题.

练习册系列答案
相关题目
2.设函数$f(x)=\left\{\begin{array}{l}{log_2}x,x>0\\{4^{-x}}+1,x≤0\end{array}\right.$,则f(2)+f(-log23)的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
19.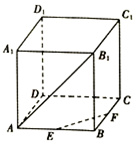 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
1.sin300°的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |