题目内容
14．已知圆x2+y2=4，点A（$\sqrt{3}$，0），动点M在圆上运动，O为坐标原点，则∠OMA的最大值为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
分析 设|MA|=x，则可求得|OM|，|AO|的值，进而利用余弦定理得到cos∠OMA的表达式，利用均值不等式求得cos∠OMA的最小值，进而求得∠OMA的最大值．
解答 解：设|MA|=x，则|OM|=2，|AO|=$\sqrt{3}$
由余弦定理可知cos∠OMA=$\frac{4+{x}^{2}-3}{4x}$=$\frac{1}{4}$（x+$\frac{1}{x}$）≥$\frac{1}{4}$×2=$\frac{1}{2}$（当且仅当x=1时等号成立）
∴∠OMA≤$\frac{π}{3}$．
故选：C．
点评 本题主要考查了点与圆的位置关系，余弦定理的应用，均值不等式求最值．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
5．设方程（m+1）|ex-1|-1=0的两根分别为x1，x2（x1＜x2），方程|ex-1|-m=0的两根分别为x3，x4（x3＜x4）．若m∈（0，$\frac{1}{2}$），则（x4+x1）-（x3+x2）的取值范围为（ ）
| A． | （-∞，0） | B． | （-∞，ln$\frac{3}{5}$） | C． | （ln$\frac{3}{5}$，0） | D． | （-∞，-1） |
9．已知在△ABC中，a、b、c分别是三个内角∠A、∠B、∠C的对边，且$\frac{sinA-sinC}{sinB}$=$\frac{sinA-sinB}{sinA+sinC}$，则∠C=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
，
，
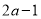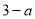．则这个数列的通项公式为_______．